%%{init: {"theme": "white", "themeVariables": {"fontSize": "48px"}, "flowchart":{"htmlLabels":false}}}%%
flowchart TD
BayesianMethods("BayesianMethods") --> MarketingDataScience("Marketing Data Science")
style BayesianMethods fill:#ff3660
style MarketingDataScience fill:#1790D0
Bayesian Methods in Modern Marketing Analytics
PyMC Labs Online Meetup - May 2023
Mathematician & Data Scientist
Webinar’s Objective
Present some selected applications of Bayesian Methods to solve marketing data science problems in the industry.
Outline
- Introduction
- Geo-Experimentation
- Media Mix Models
- Customer Lifetime Value
- Causal Inference
- Revenue-Retention Modeling
- References
Applied Data Science
%%{init: {"theme": "white", "themeVariables": {"fontSize": "48px"}, "flowchart":{"htmlLabels":false}}}%%
flowchart TD
BusinessProblem("Business Problem") --> Model("Model")
Model --> Product("Product")
Product --> Measure("Measure")
Measure --> Stakeholders("Stakeholders")
Stakeholders --> BusinessProblem
style Model fill:#a0cdf7
Bayesian Methods
We need to explicitly describe our assumptions through the data-generating process.
Allow to include domain knowledge and constraints through priors.
Flexibility.
Uncertainty quantification.
Geo-Experimentation
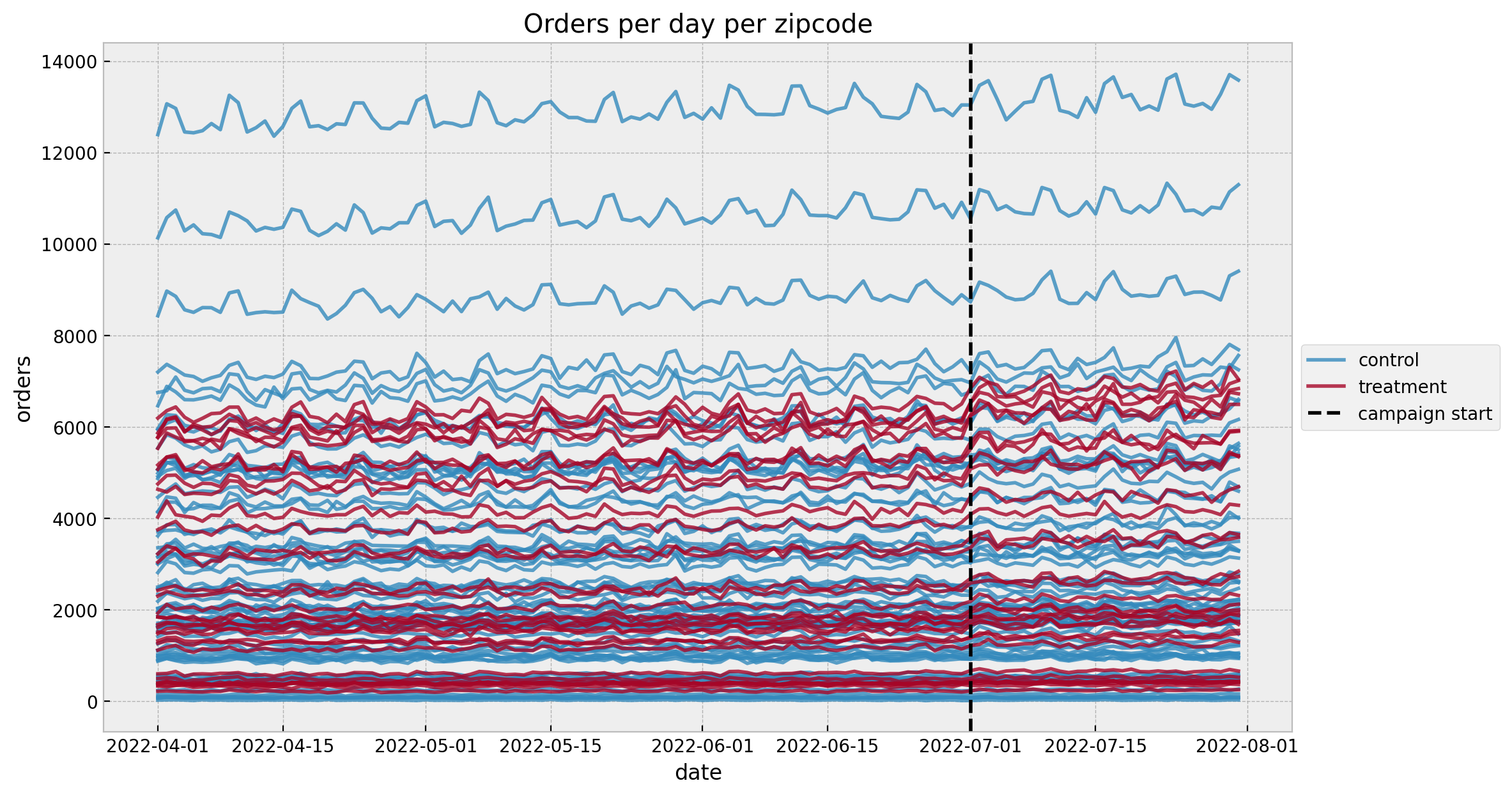
Time-Based Regression
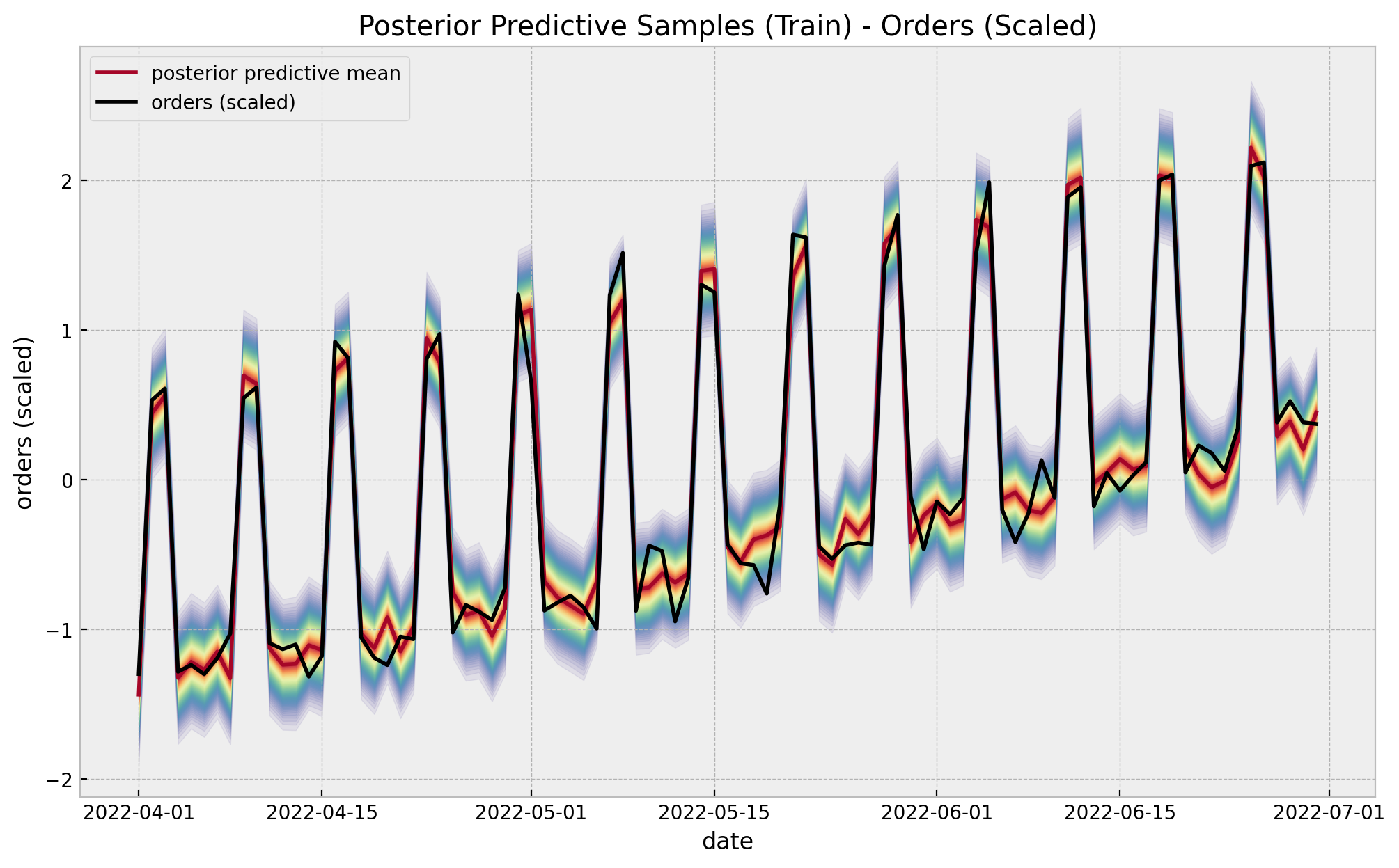
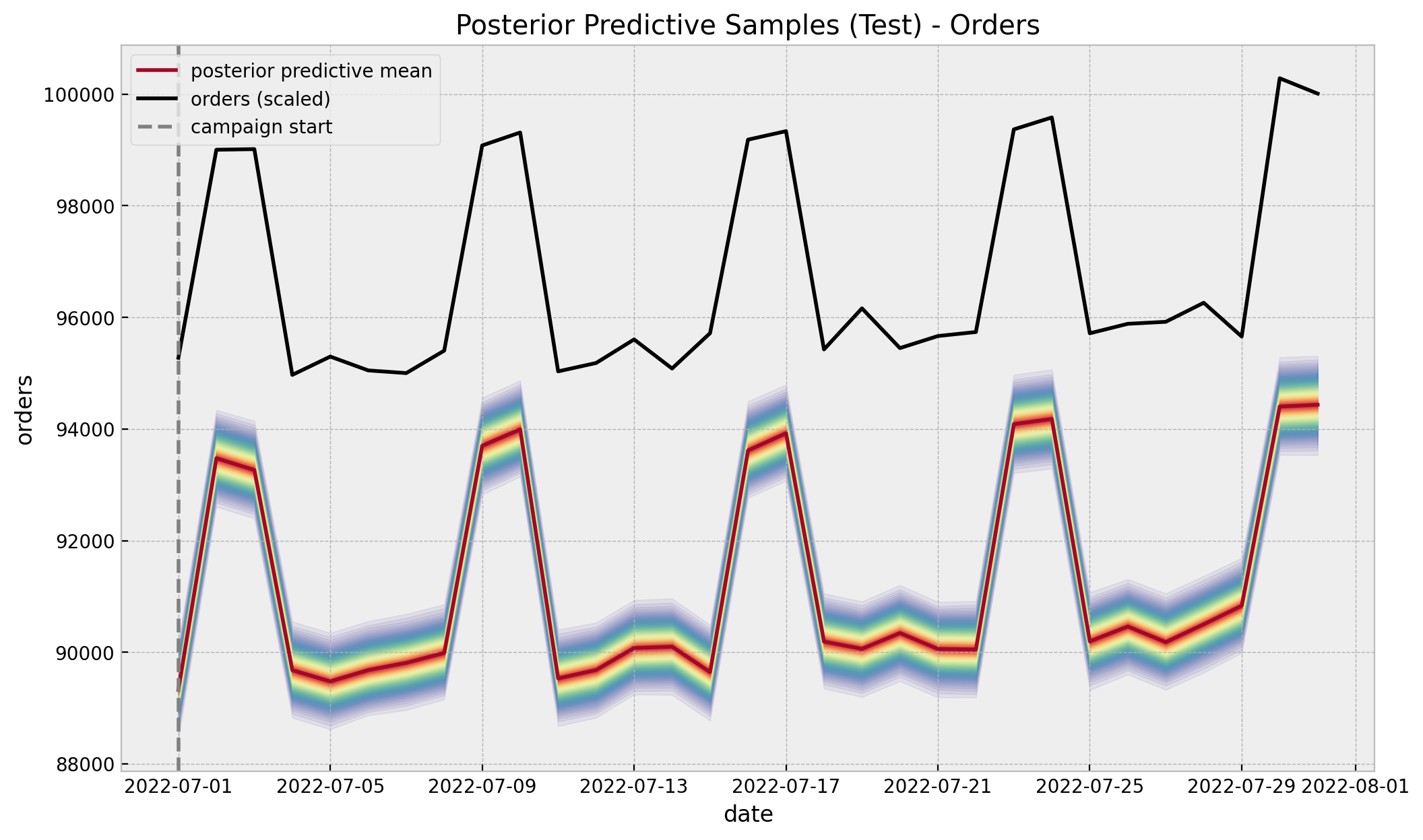
Regression Model in PyMC
with pm.Model() as model:
# --- Data Containers ---
model.add_coord(name="date", values=date_train, mutable=True)
y_control_data = pm.MutableData(
name="y_control_data", value=y_control_train_scaled, dims="date"
)
y_treatment_data = pm.MutableData(
name="y_treatment_data", value=y_treatment_train_scaled, dims="date"
)
# --- Priors ---
intercept = pm.Normal(name="intercept", mu=0, sigma=1)
beta = pm.HalfNormal(name="beta", sigma=2)
sigma = pm.HalfNormal(name="sigma", sigma=2)
nu = pm.Gamma(name="nu", alpha=20, beta=2)
# --- Model Parametrization ---
mu = pm.Deterministic(
name="mu", var=intercept + beta * y_control_data, dims="date"
)
# --- Likelihood ---
pm.StudentT(
name="likelihood", mu=mu, nu=nu, sigma=sigma, observed=y_treatment_data, dims="date"
)Marketing Measurement
%%{init: {"theme": "white", "themeVariables": {"fontSize": "48px"}, "flowchart":{"htmlLabels":false}}}%%
flowchart LR
Experimentation("Experimentation") --> MMM("Media Mix Model")
MMM --> Attribution("Attribution")
Attribution --> Experimentation
Media Mix Models
Media Mix Models (MMM) are used by advertisers to measure the effectiveness of their advertising and provide insights for making future budget allocation decisions.
Media mix models are also used to find the optimal media mix that maximizes the revenue under a budget constraint in the selected time period.
Media Transformations
Carryover (Adstock) & Saturation
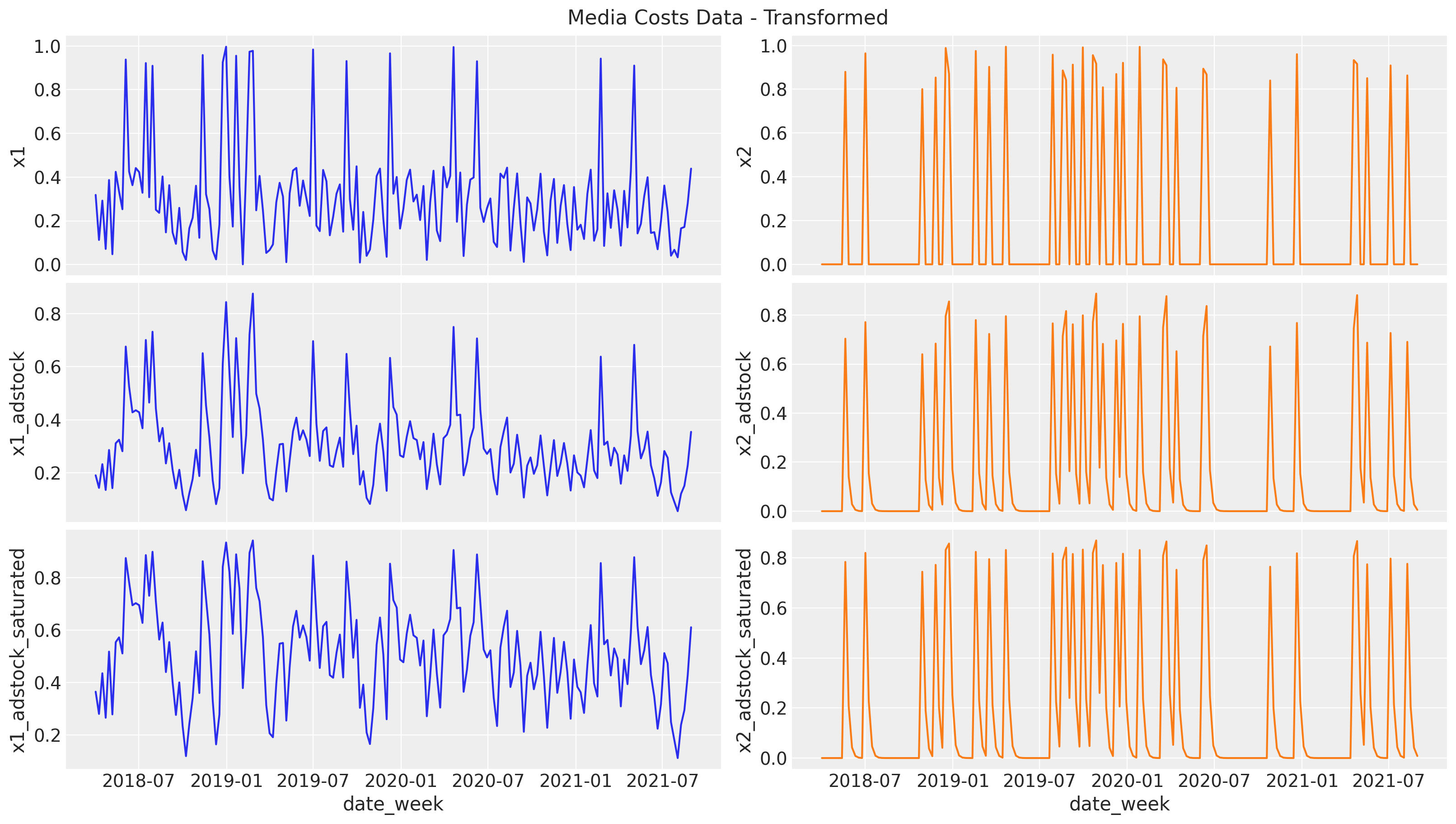
Media Mix Model Target
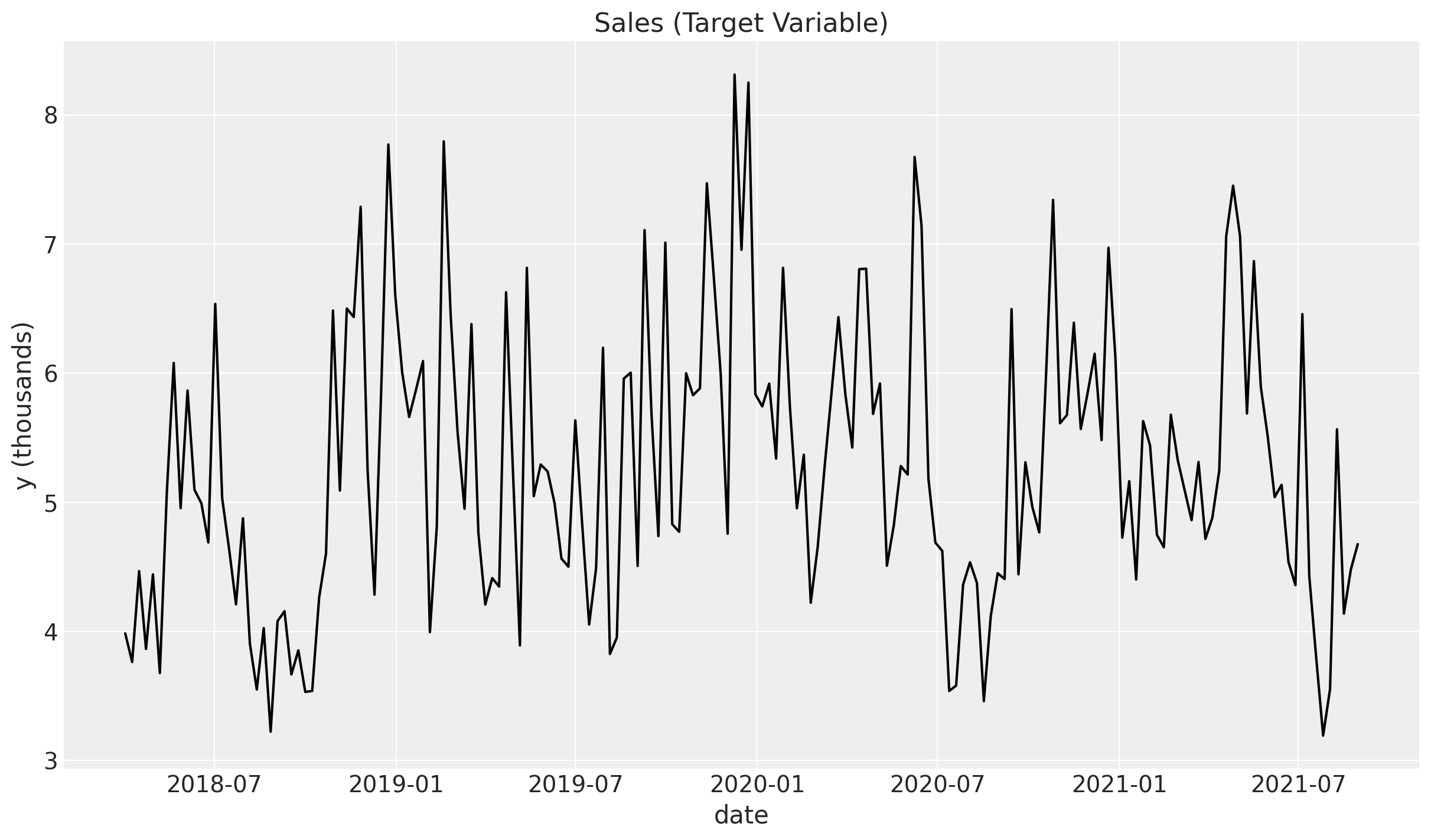
We want to understand the contribution of channels \(x_1\) and \(x_2\) spend into the target variable sales.
MMM Structure

Media Contribution Estimation
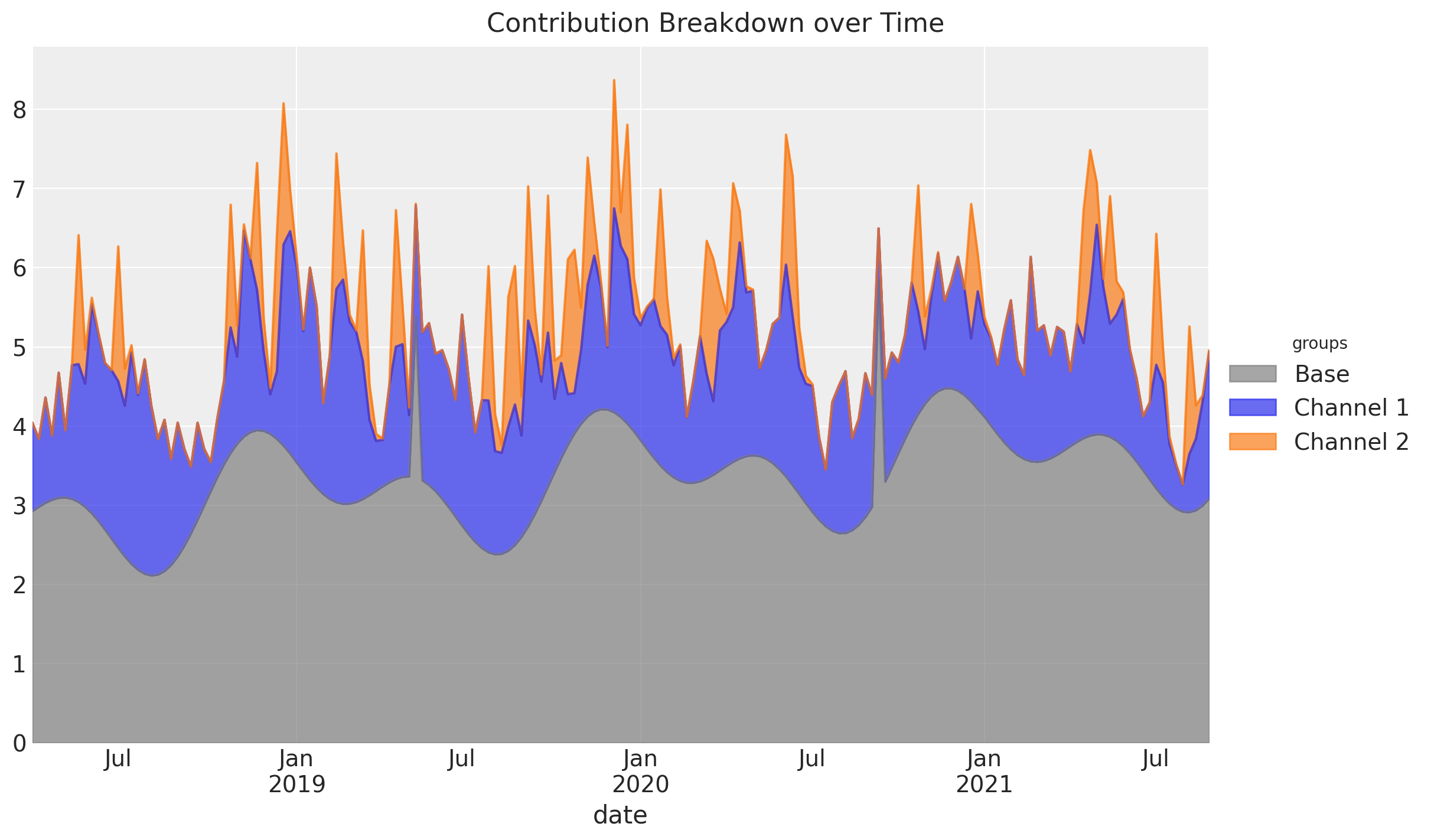
Budget Optimization
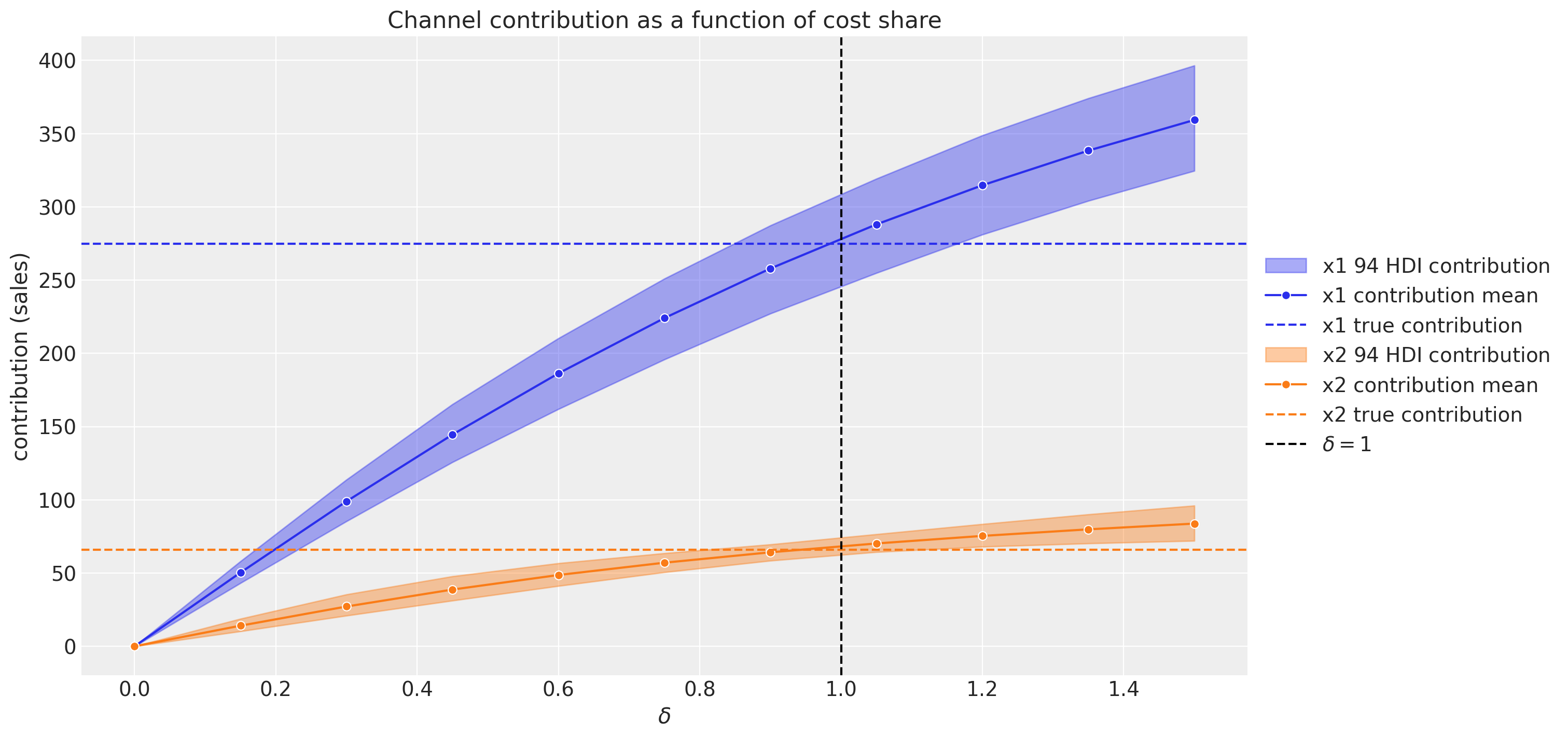
See pymc-marketing, Issue 259
PyMC-Marketing
Bayesian marketing toolbox in PyMC. Media Mix (MMM), customer lifetime value (CLV), buy-till-you-die (BTYD) models and more.

PyMC-Marketing - More MMM Flavours
Very ambitious plans! E.g. Time-varying coefficients through hierarchical Gaussian Processes
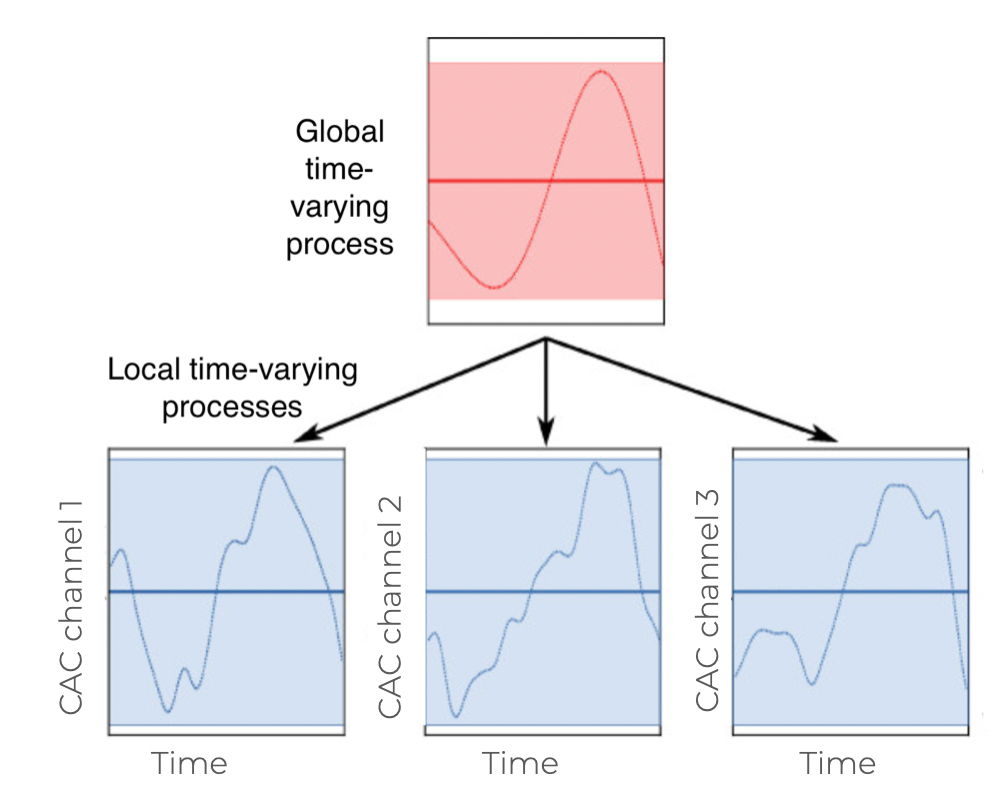
Customer Lifetime Value (CLV)
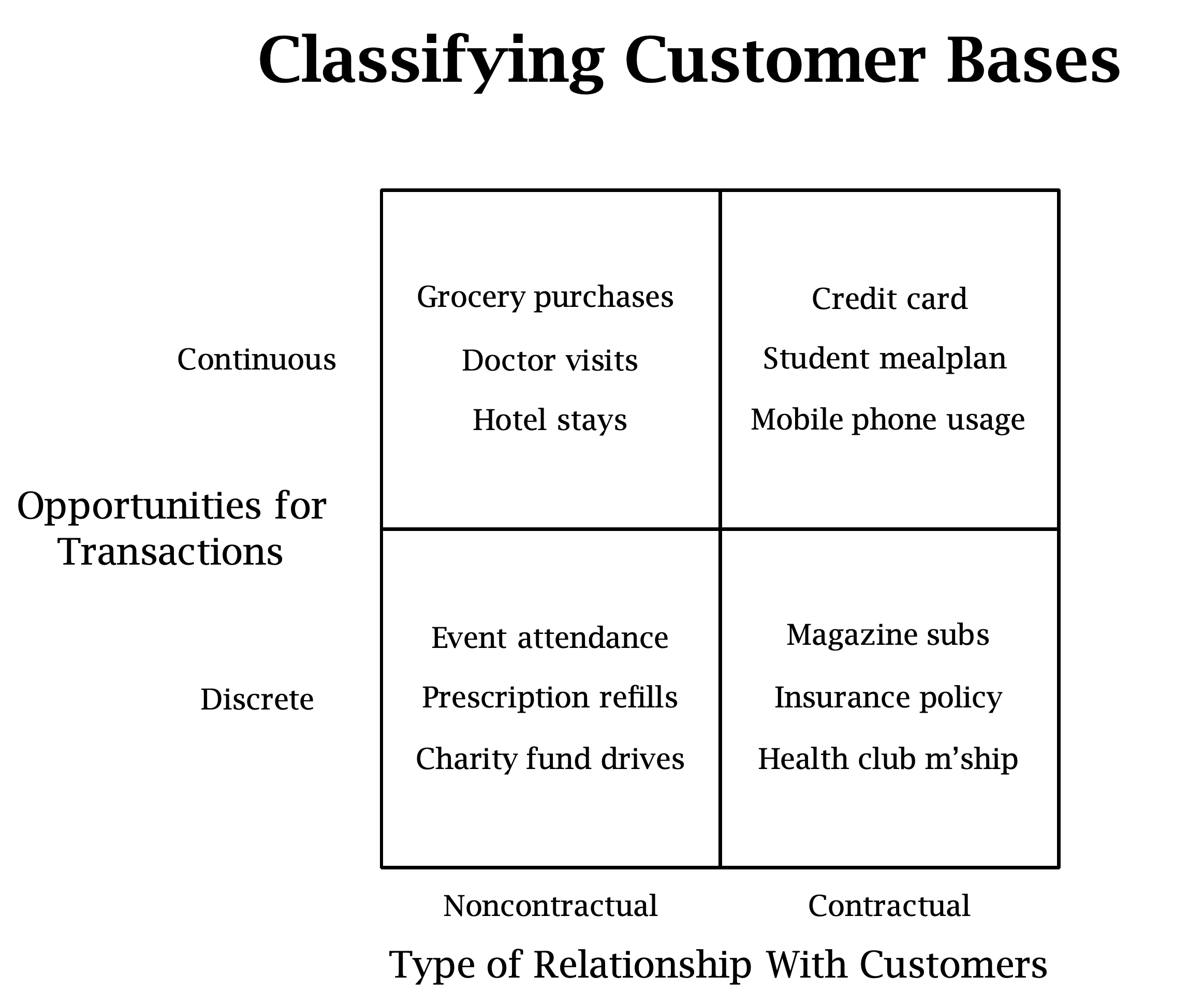
Continuous Non-Contractractual CLV
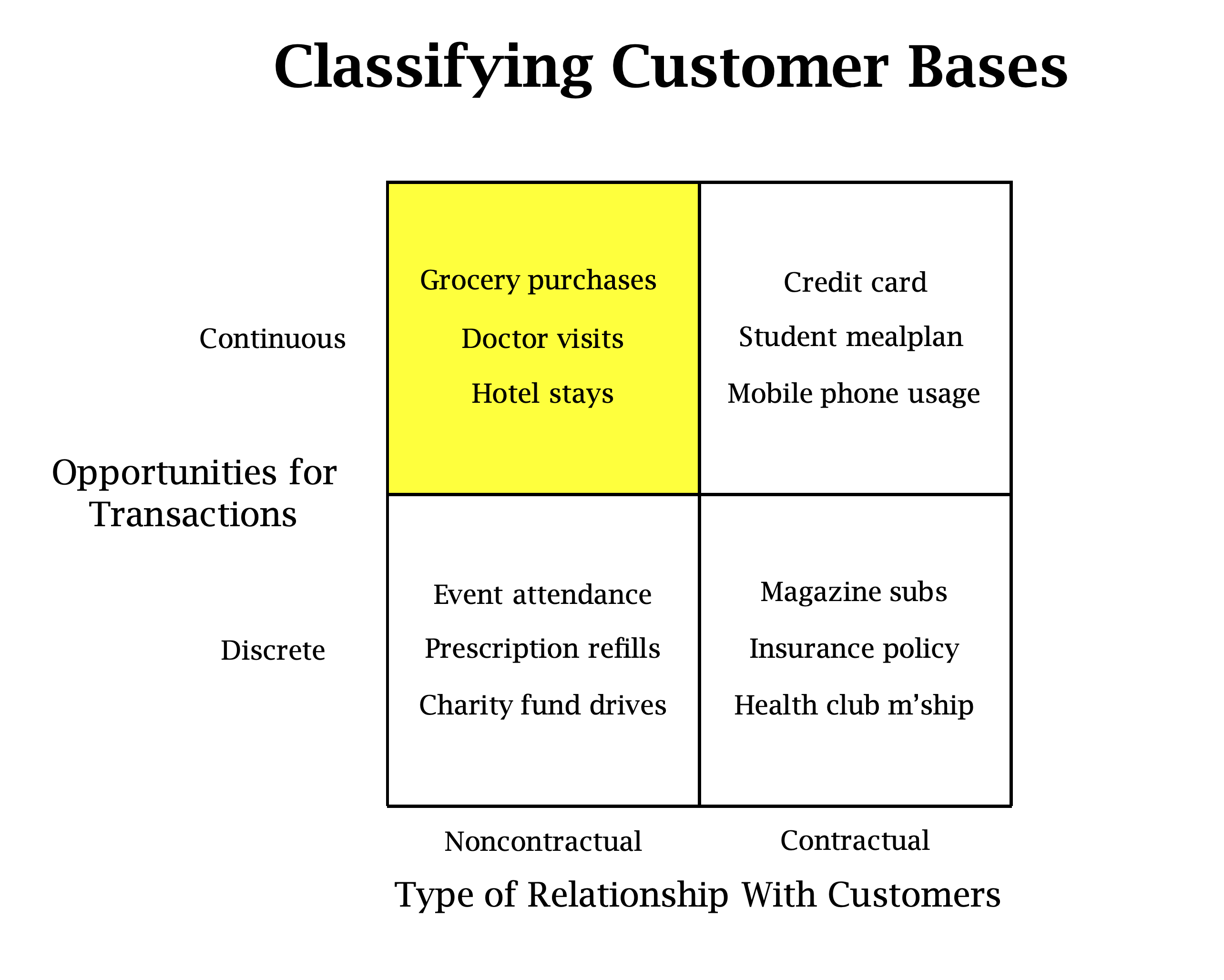
frequency: Number of repeat purchases the customer has made.T: Age of the customer in whatever time units chosen.recency: Age of the customer when they made their most recent purchases.
CLV Estimation Strategy
%%{init: {"theme": "dark", "themeVariables": {"fontSize": "48px"}, "flowchart":{"htmlLabels":false}}}%%
flowchart LR
Recency("Recency") --> BGNBD(["BG/NBD"])
T("T") --> BGNBD
Frequency("Frequency") --> BGNBD
Recency("Recency") --> GammaGamma(["Gamma-Gamma"])
T --> GammaGamma
Frequency("Frequency") --> GammaGamma
MonetaryValue("Monetary Value") --> GammaGamma
BGNBD --> ProbabilityAlive("Probability Alive")
BGNBD --> PurchasePrediction("Purchase Prediction")
GammaGamma --> MonetaryValuePrediction("Monetary Value Prediction")
PurchasePrediction --> CLV(("CLV"))
MonetaryValuePrediction --> CLV
style BGNBD fill:#ff3660
style GammaGamma fill:#ff3660
style ProbabilityAlive fill:#1790D0
style PurchasePrediction fill:#1790D0
style MonetaryValuePrediction fill:#1790D0
style CLV fill:#0bb09d
BG/NBD Assumptions
While active, the time between transactions is distributed exponentially with transaction rate, i.e.,
\[f(t_{j}|t_{j-1}; \lambda) = \lambda \exp(-\lambda (t_{j} - t_{j - 1})), \quad t_{j} \geq t_{j - 1} \geq 0\]
Heterogeneity in \(\lambda\) follows a gamma distribution with pdf
\[f(\lambda|r, \alpha) = \frac{\alpha^{r}\lambda^{r - 1}\exp(-\lambda \alpha)}{\Gamma(r)}, \quad \lambda > 0\]
After any transaction, a customer becomes inactive with probability \(p\).
Heterogeneity in \(p\) follows a beta distribution with pdf
\[f(p|a, b) = \frac{\Gamma(a + b)}{\Gamma(a) \Gamma(b)} p^{a - 1}(1 - p)^{b - 1}, \quad 0 \leq p \leq 1\]
The transaction rate \(\lambda\) and the dropout probability \(p\) vary independently across customers.
BG/NBD - Parameter Estimation
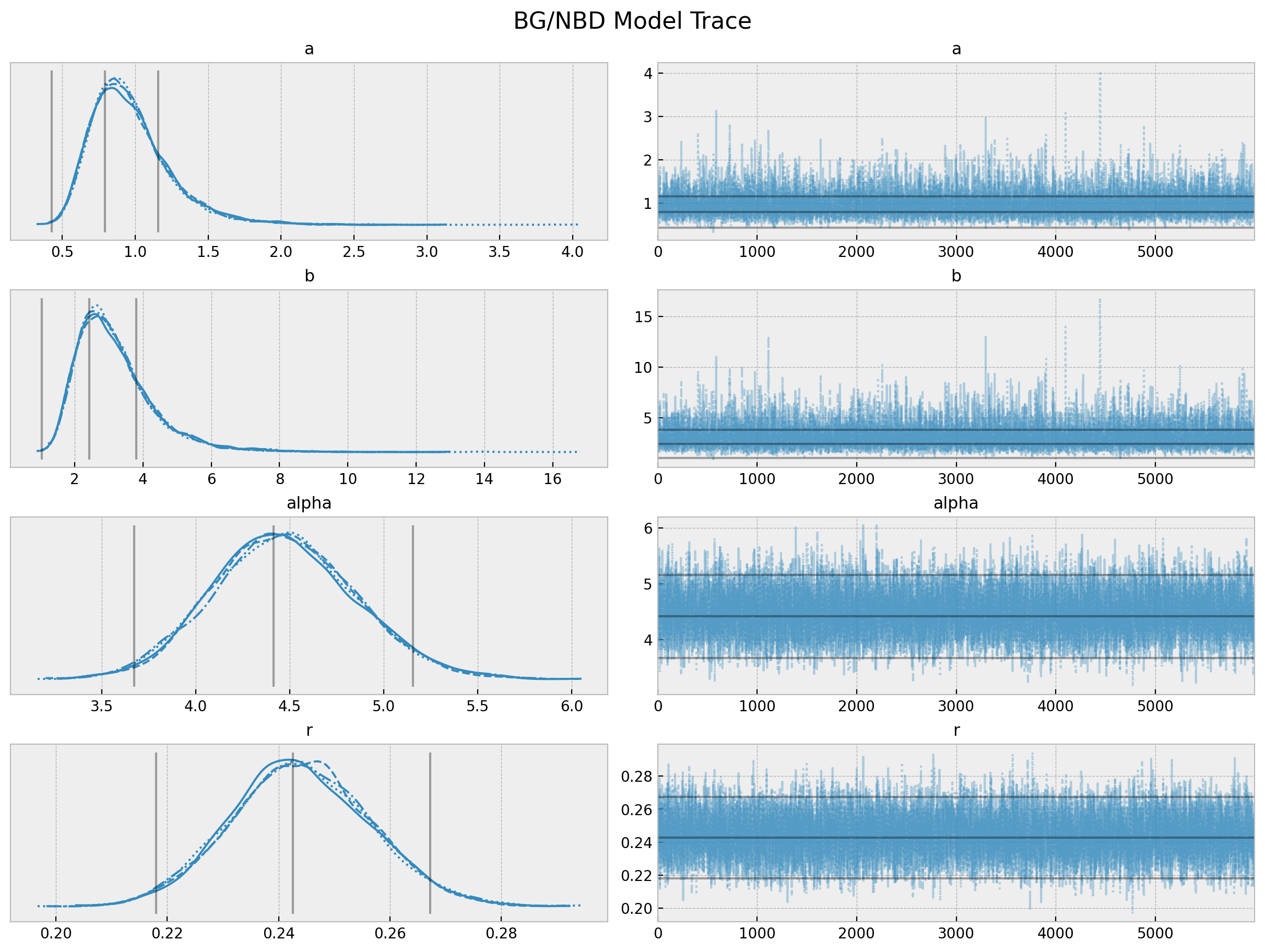
BG/NBD - Probability of Alive
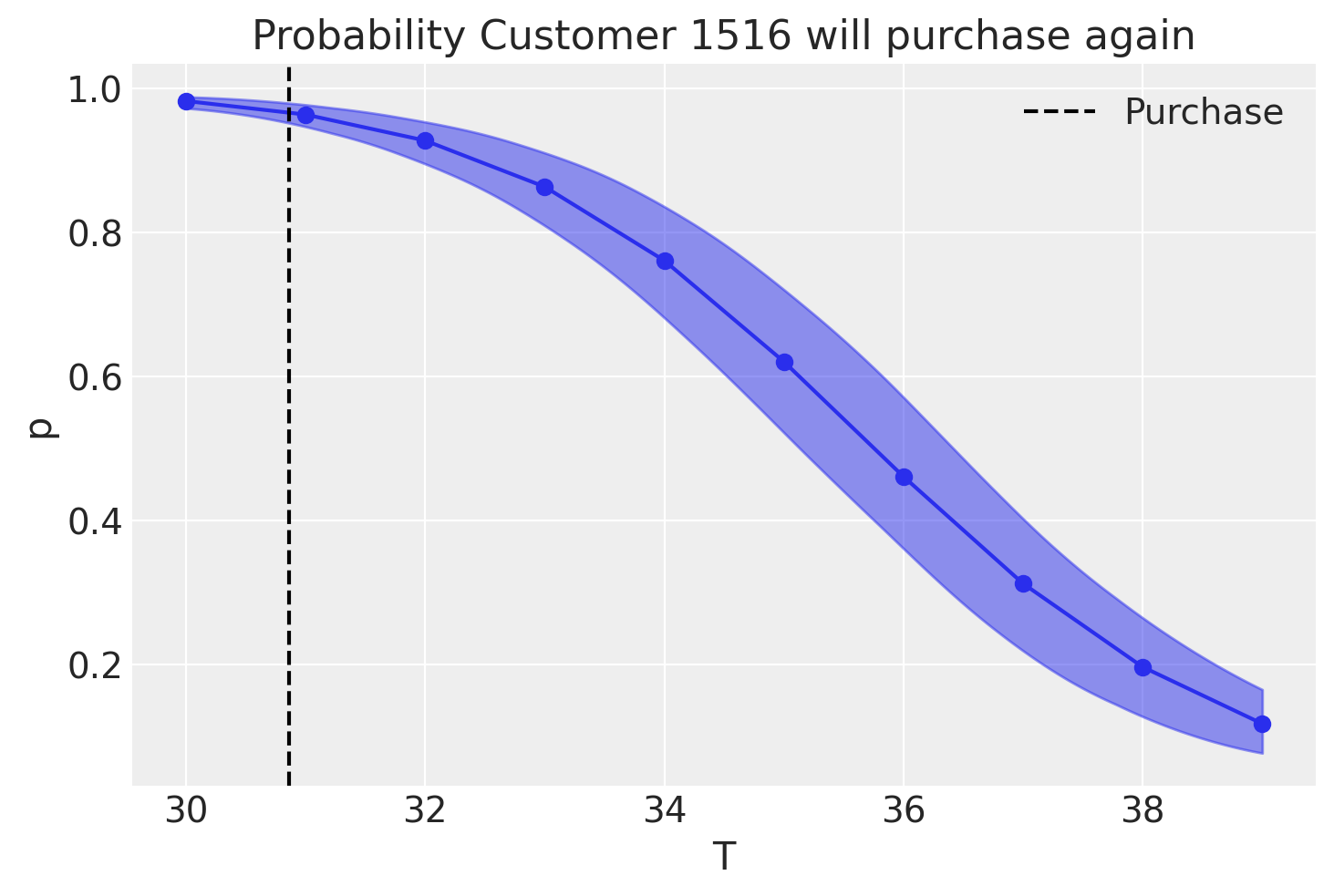
Gamma-Gamma Model
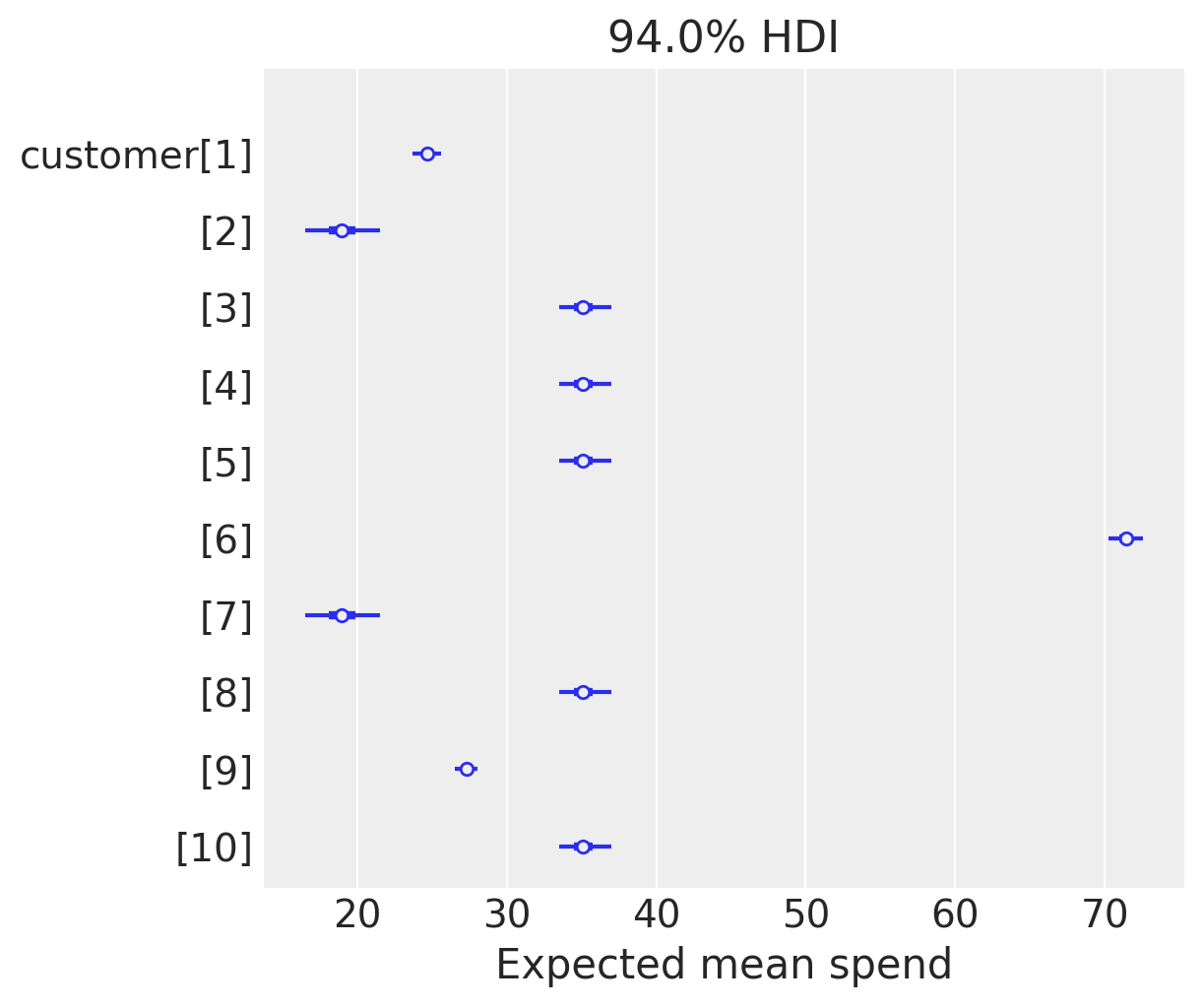
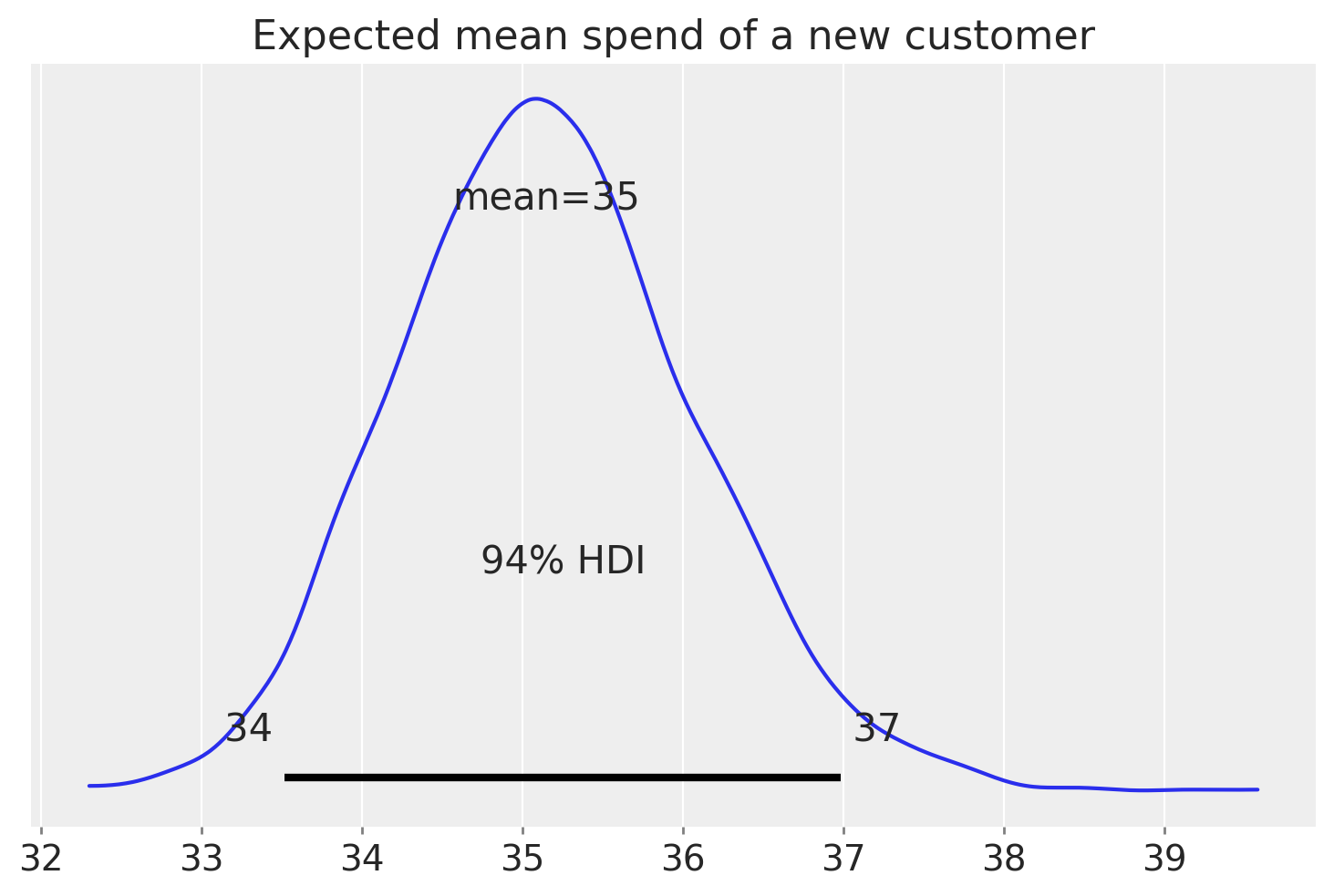
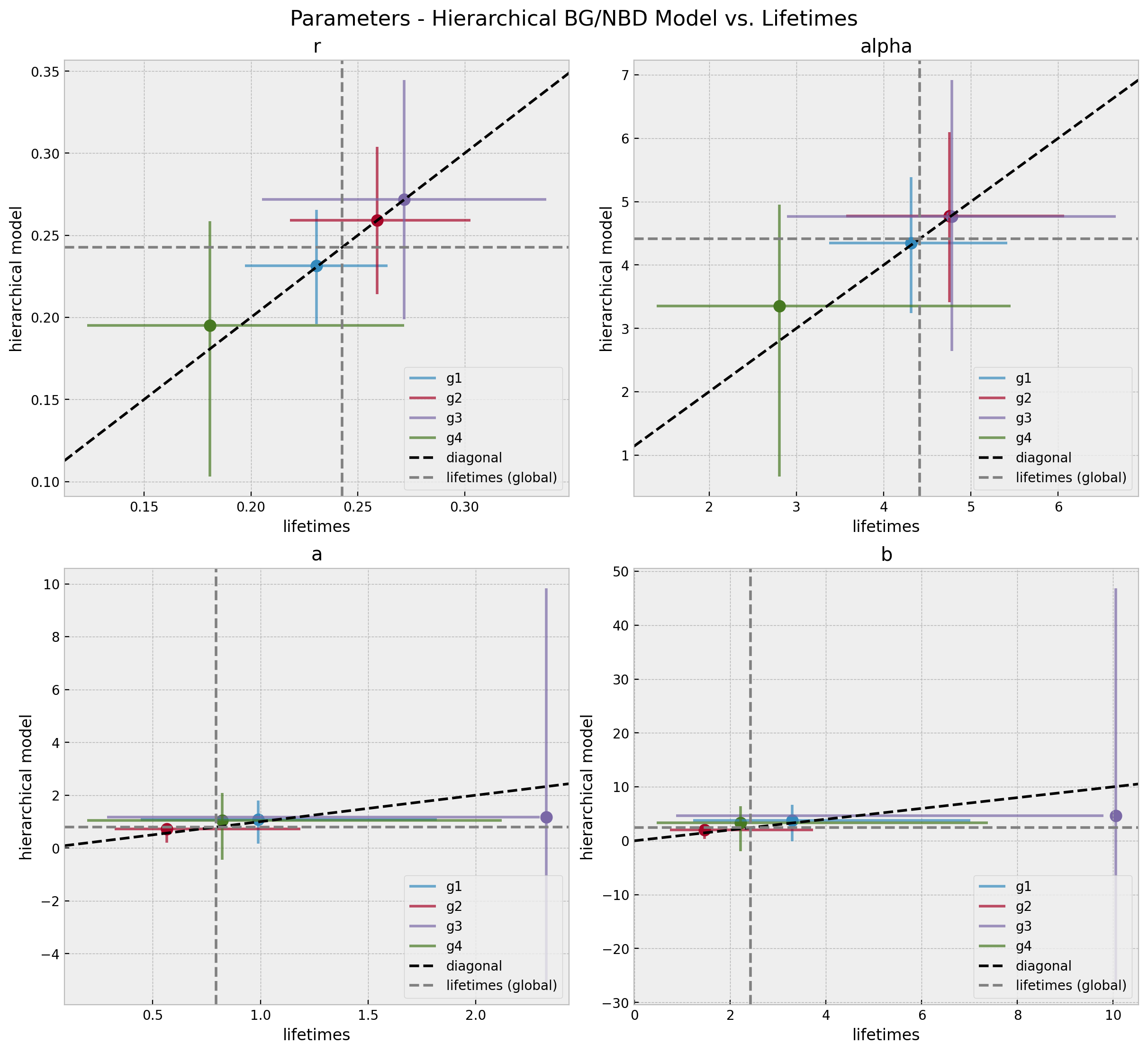
BG/NBD - Hierarchical Models
Causal Inference
Synthetic Control
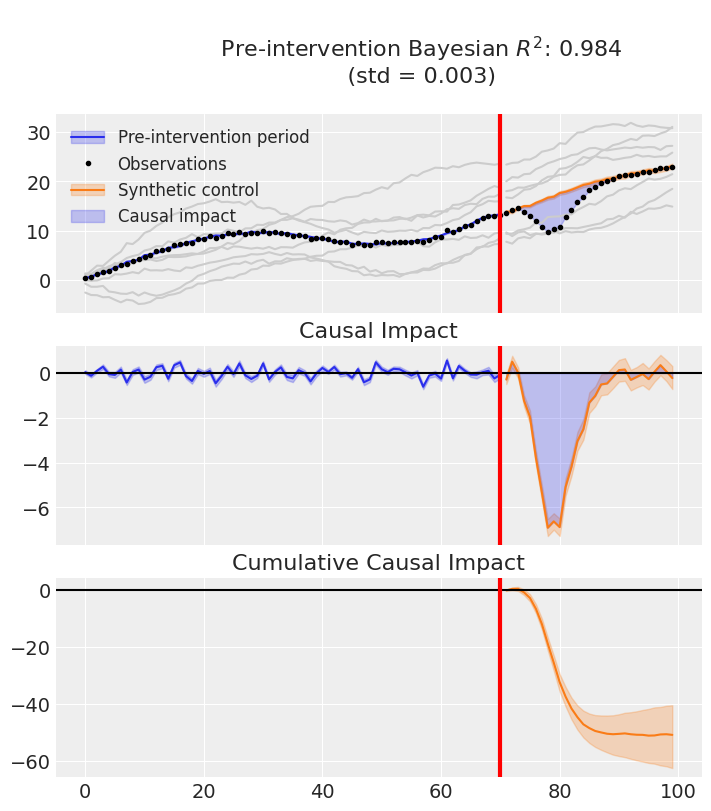

Causal Inference
Difference-in-Differences
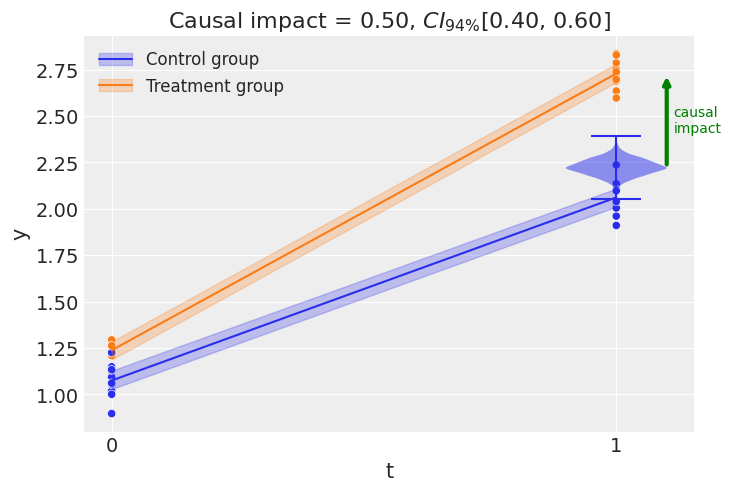
Regression Discontinuity
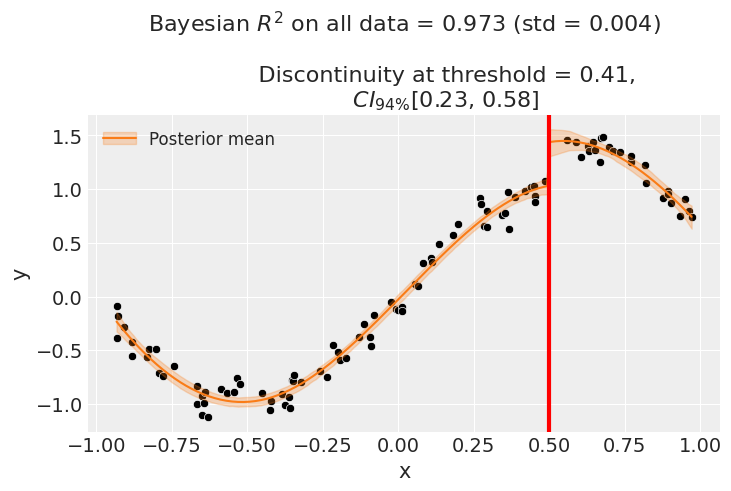
Instrumental Variables

Cohort Revenue-Retention Modeling
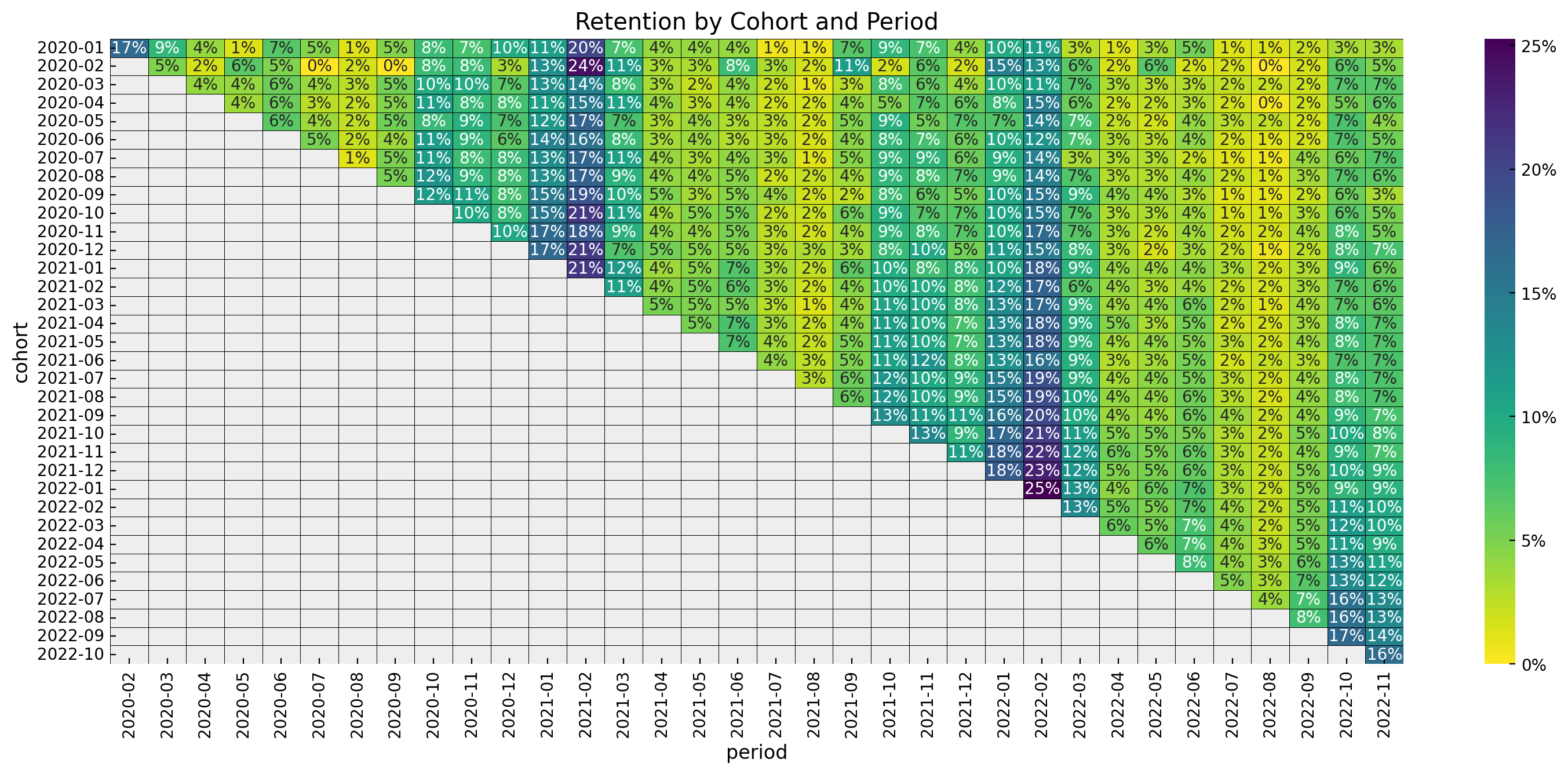
- Cohort Age: Age of the cohort in months.
- Age: Age of the cohort with respect to the observation time.
- Month: Month of the observation time (period).
Retention Component
\[\begin{align*} \textrm{logit}(p) & = \text{BART}(\text{cohort age}, \text{age}, \text{month}) \\ N_{\text{active}} & \sim \text{Binomial}(N_{\text{total}}, p) \end{align*}\]
Revenue Component
\[\begin{align*} \log(\lambda) = \: (& \text{intercept} \\ & + \beta_{\text{cohort age}} \text{cohort age} \\ & + \beta_{\text{age}} \text{age} \\ & + \beta_{\text{cohort age} \times \text{age}} \text{cohort age} \times \text{age}) \\ \text{Revenue} & \sim \text{Gamma}(N_{\text{active}}, \lambda) \end{align*}\]
Cohot Revenue-Retention Model
mu = pmb.BART(name="mu", X=x, Y=train_retention_logit, m=50, dims="obs")
p = pm.Deterministic(name="p", var=pm.math.invlogit(mu), dims="obs")
lam_log = pm.Deterministic(
name="lam_log",
var=intercept
+ b_age_scaled * age_scaled
+ b_cohort_age_scaled * cohort_age_scaled
+ b_age_cohort_age_interaction * age_scaled * cohort_age_scaled,
dims="obs",
)
lam = pm.Deterministic(name="lam", var=pm.math.exp(lam_log), dims="obs")
n_active_users_estimated = pm.Binomial(
name="n_active_users_estimated",
n=n_users,
p=p,
observed=n_active_users,
dims="obs",
)
x = pm.Gamma(
name="revenue_estimated",
alpha=n_active_users_estimated + eps,
beta=lam,
observed=revenue,
dims="obs",
)Cohort Revenue-Retention Model

Revenue-Retention - Predictions
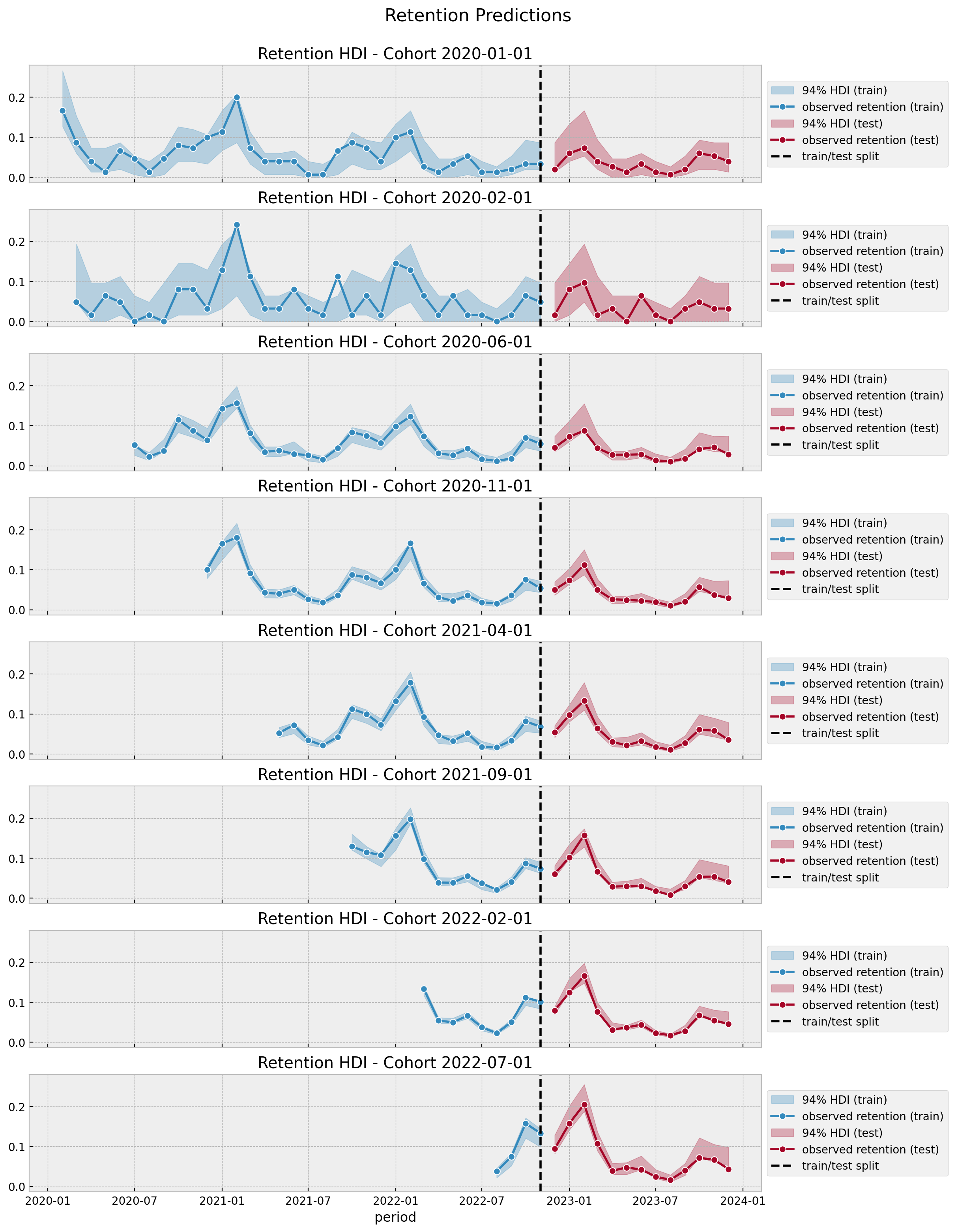
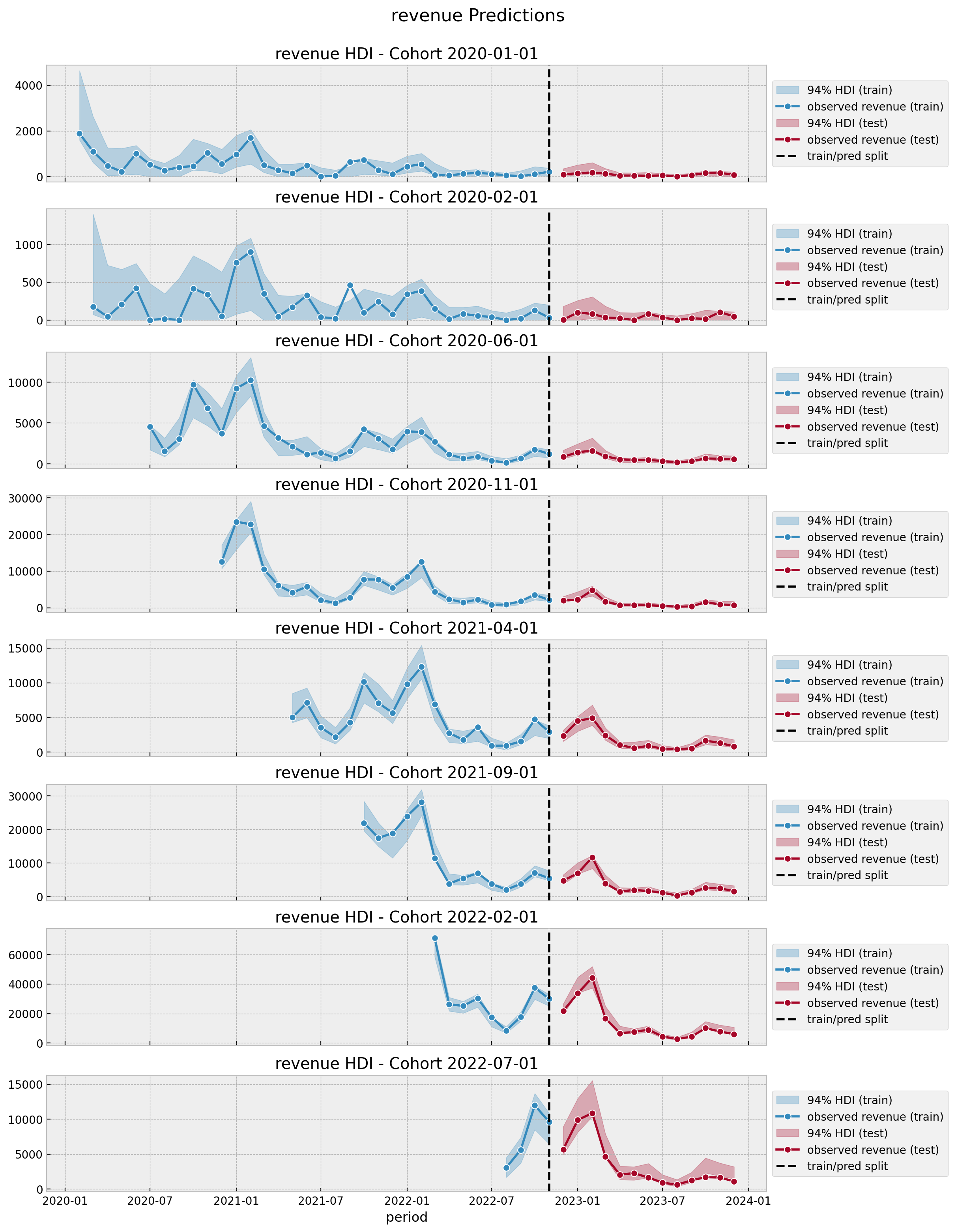
References
Media Mix Models
Bayesian Methods for Media Mix Modeling with Carryover and Shape Effects
PyMC bayesian model details: Media Effect Estimation with PyMC: Adstock, Saturation & Diminishing Returns
pymc-marketing: Bayesian marketing toolbox in PyMC. Media Mix (MMM), customer lifetime value (CLV), buy-till-you-die (BTYD) models and more.Bayesian Media Mix Models: Modelling changes in marketing effectiveness over time, by PyMC Labs
Customer Lifetime Value
References
Geo-Experimentaton
Causal Inference
CausalPy: A Python package for causal inference in quasi-experimental settingsExperimentation, Non-Compliance and Instrumental Variables with PyMC
Revenue-Retention Modeling
Thank you!

Connect with PyMC Labs
🔗 Learn more about pymc-marketing:
- 🐙 GitHub: https://github.com/pymc-labs/pymc-marketing
- 📝 Documentation: https://www.pymc-marketing.io/en/stable/
🔗 Connecting with PyMC Labs:
- 👥 LinkedIn: https://www.linkedin.com/company/pymc-labs/
- 🐦 Twitter: https://twitter.com/pymc_labs
- 🎥 YouTube: https://www.youtube.com/PyMCLabs
- 🤝 Meetup: https://www.meetup.com/pymc-labs-online-meetup/
