Cohort Revenue & Retention Analysis: A Bayesian Approach

Machine Learning Week - 2023

Dr. Juan Orduz

Mathematician & Data Scientist

Outline

1. Introduction: Business Problem (retention)

2. Some Bottom-Up Approaches

3. Simple Cohort Retention Model (GLM)

4. Retention Model with BART

5. Cohort Revenue-Retention Model

6. Applications

7. References

Business Problem

Example

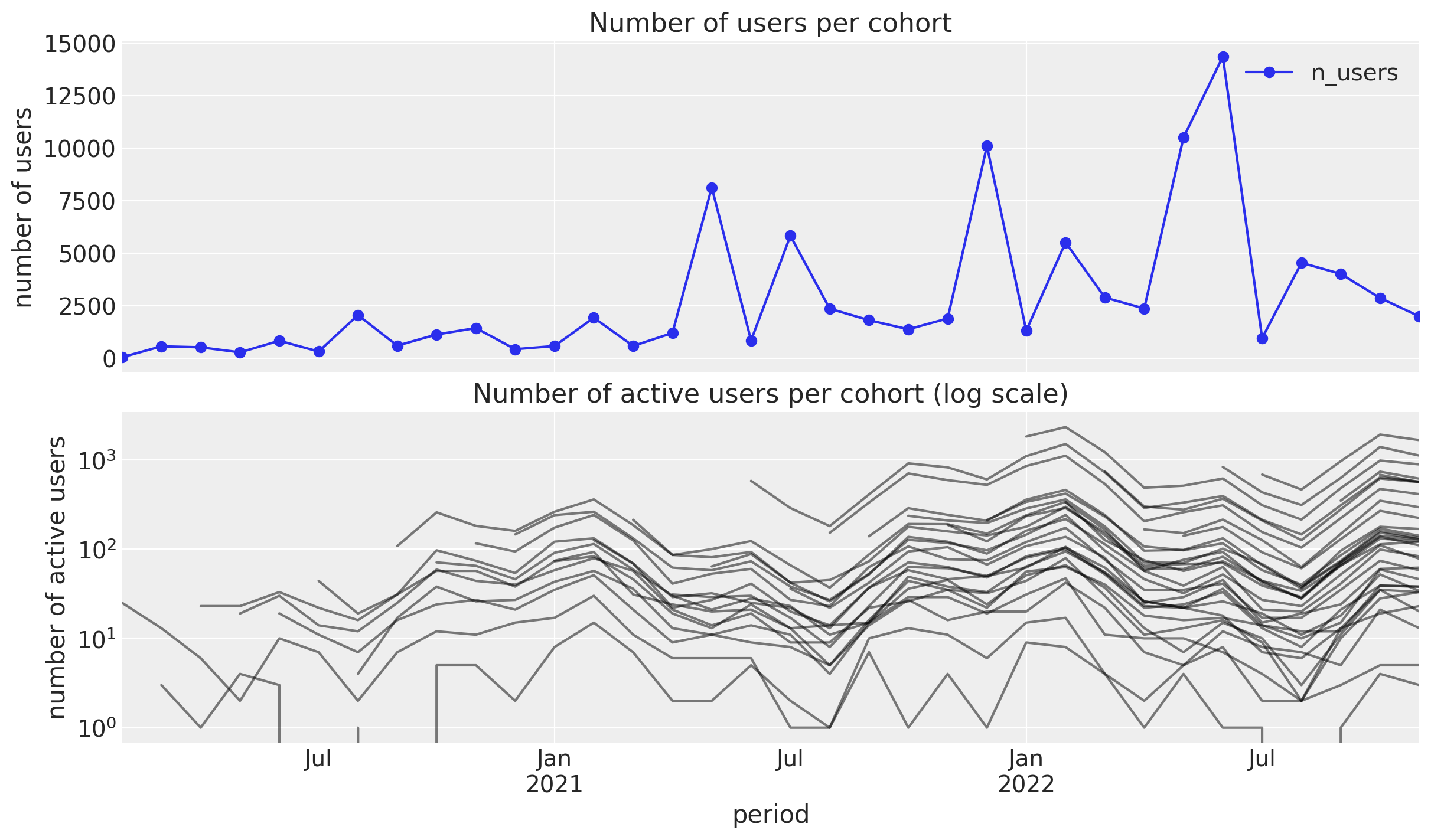
• During January \(2020\), \(100\) users signed up for a service (cohort).

• In February \(2020\), there were \(17\) users from the \(2020-01\) cohort active (e.g. did at least one purchase). The retention rate is \(17\%\).

• We want to understand and predict how retention develops over time.

• The main motivation is to estimate customer lifetime value (CLV).

Number of Active Users

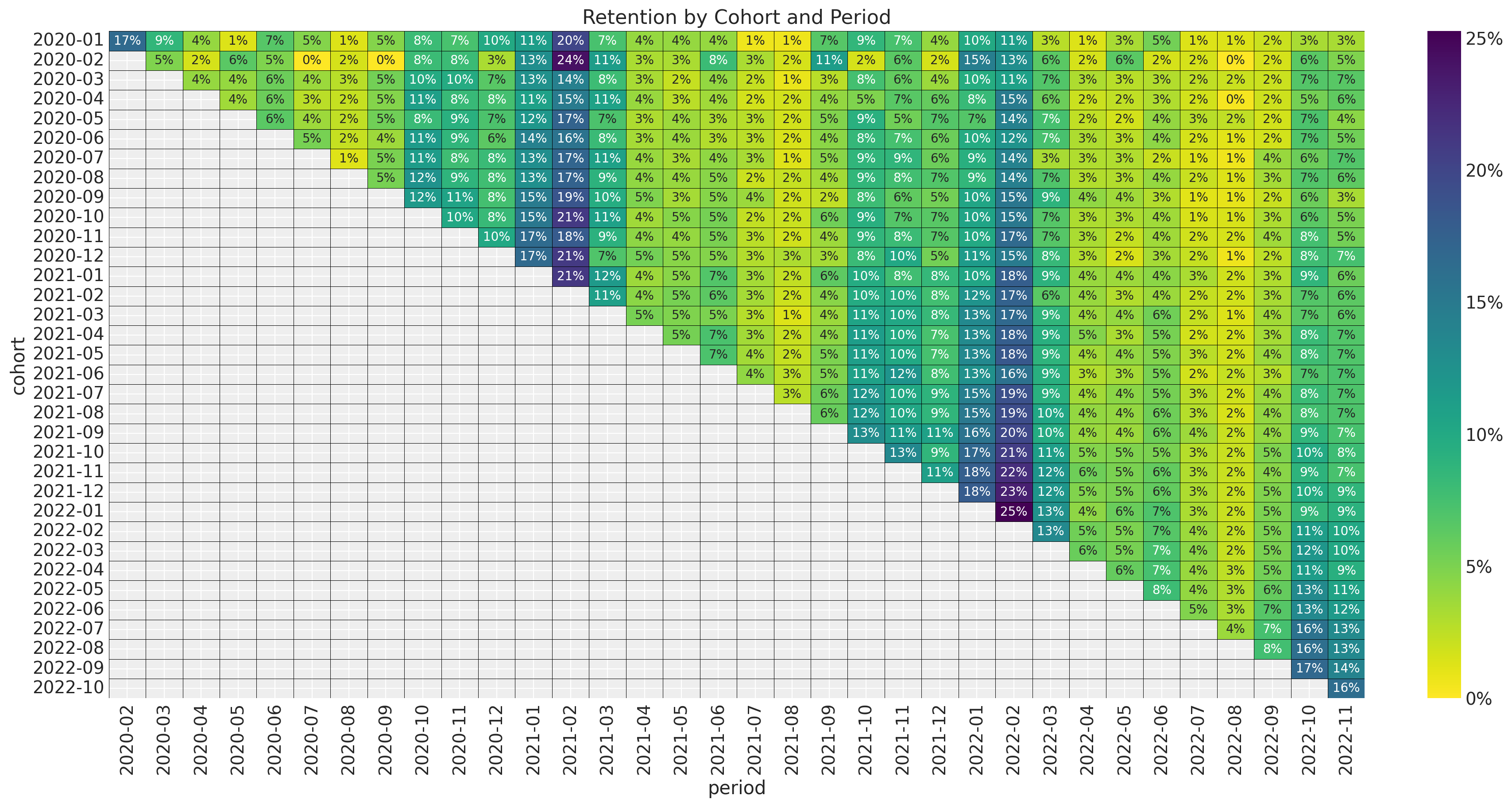
Retention Matrix

Some Bottom-Up Approaches

Shifted Beta Geometric (Contractual)

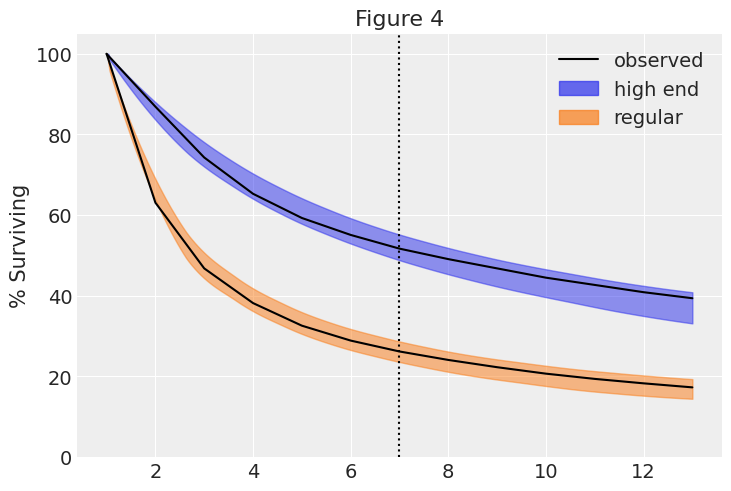
• An individual remains a customer of the company with constant retention probability \(1 - \theta\).

• Heterogeneity: \(\theta \sim \text{Beta}(a, b)\).

BG/NBD Model (Non-Contractual)

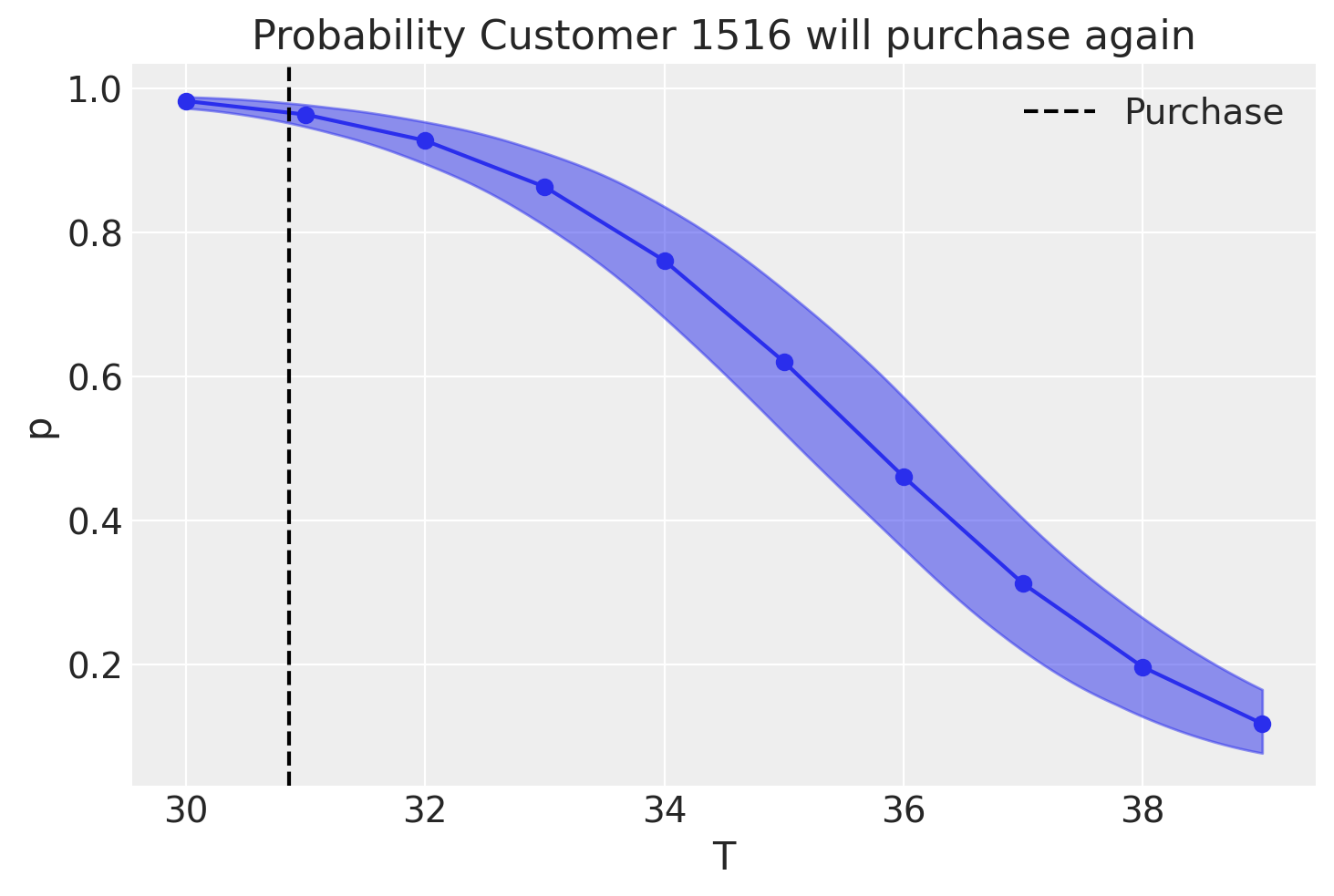
• Transaction process: \(\lambda \sim \text{Gamma}(r, \alpha)\).
• Dropout probability: \(p \sim \text{Beta}(a, b)\).

Model the Retention Matrix 💡

• Cohort Age: Age of the cohort in months.
• Age: Age of the cohort with respect to the observation time.
• Month: Month of the observation time (period).

Retention Over Time (period)

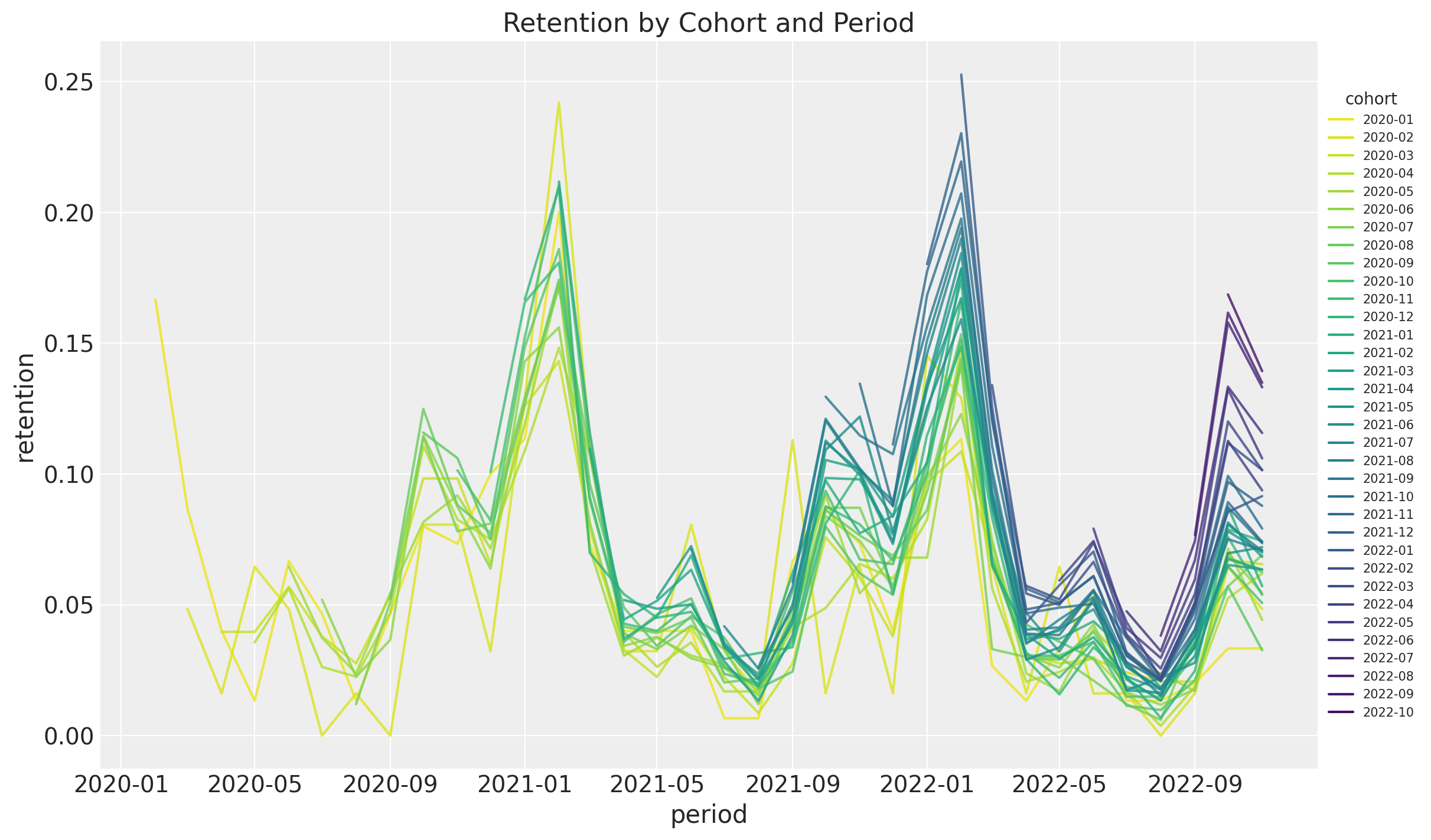
Modeling Strategy: Close cohorts behave similarly.

Retention - Generalized Linear Model

\[\begin{align*} N_{\text{active}} \sim & \: \text{Binomial}(N_{\text{total}}, p) \\ \textrm{logit}(p) = & \: ( \text{intercept} \\ & + \beta_{\text{cohort age}} \text{cohort age} \\ & + \beta_{\text{age}} \text{age} \\ & + \beta_{\text{cohort age} \times \text{age}} \text{cohort age} \times \text{age} \\ & + \beta_{\text{seasonality}} \text{seasonality} ) \end{align*}\]

where \(p\) represents the retention and \(\text{logit}: (0, 1) \longrightarrow \mathbb{R}\) is defined by \(\text{logit}(p) = \log\left(\frac{p}{1-p}\right)\).

Retention - GLM in PyMC

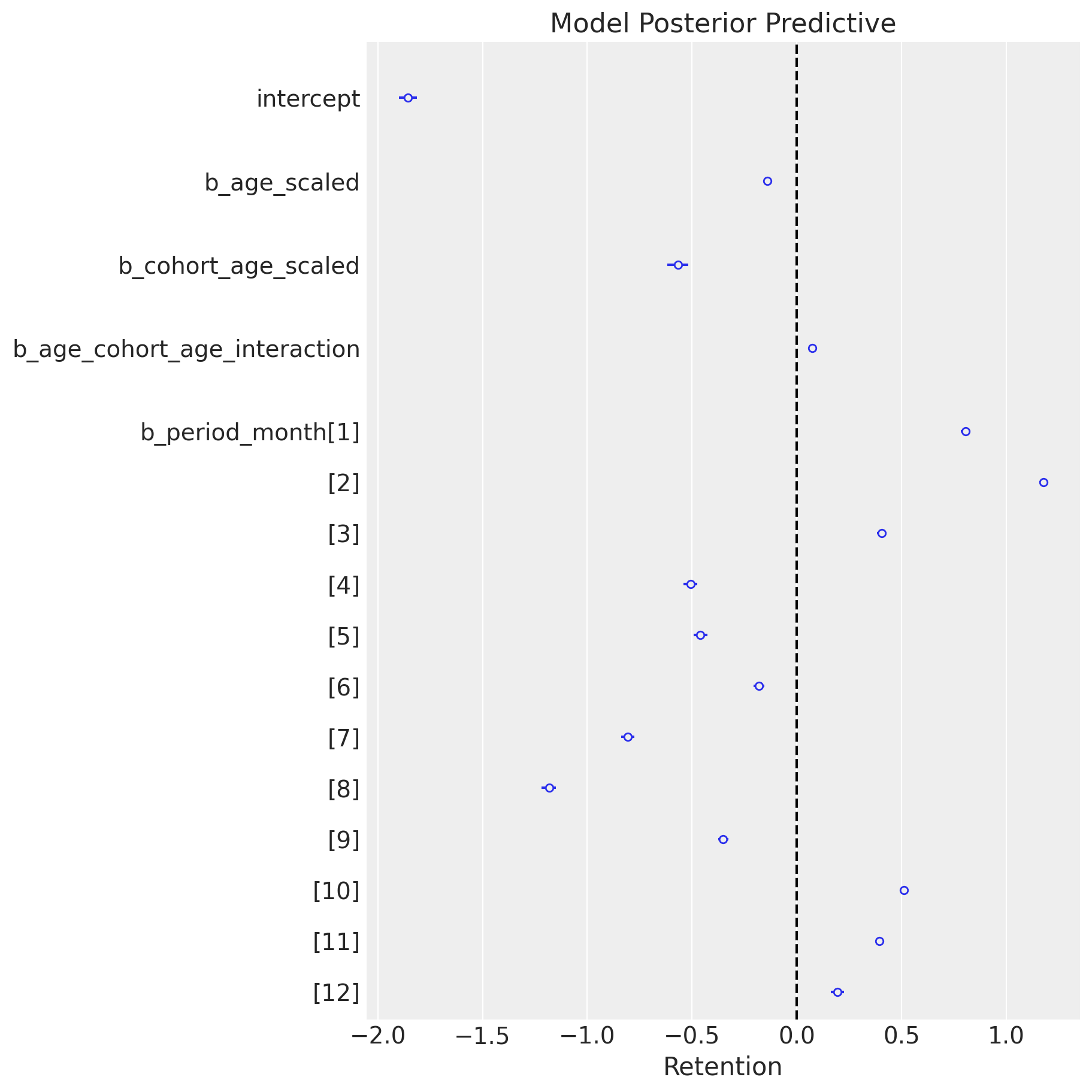
Posterior Distribution

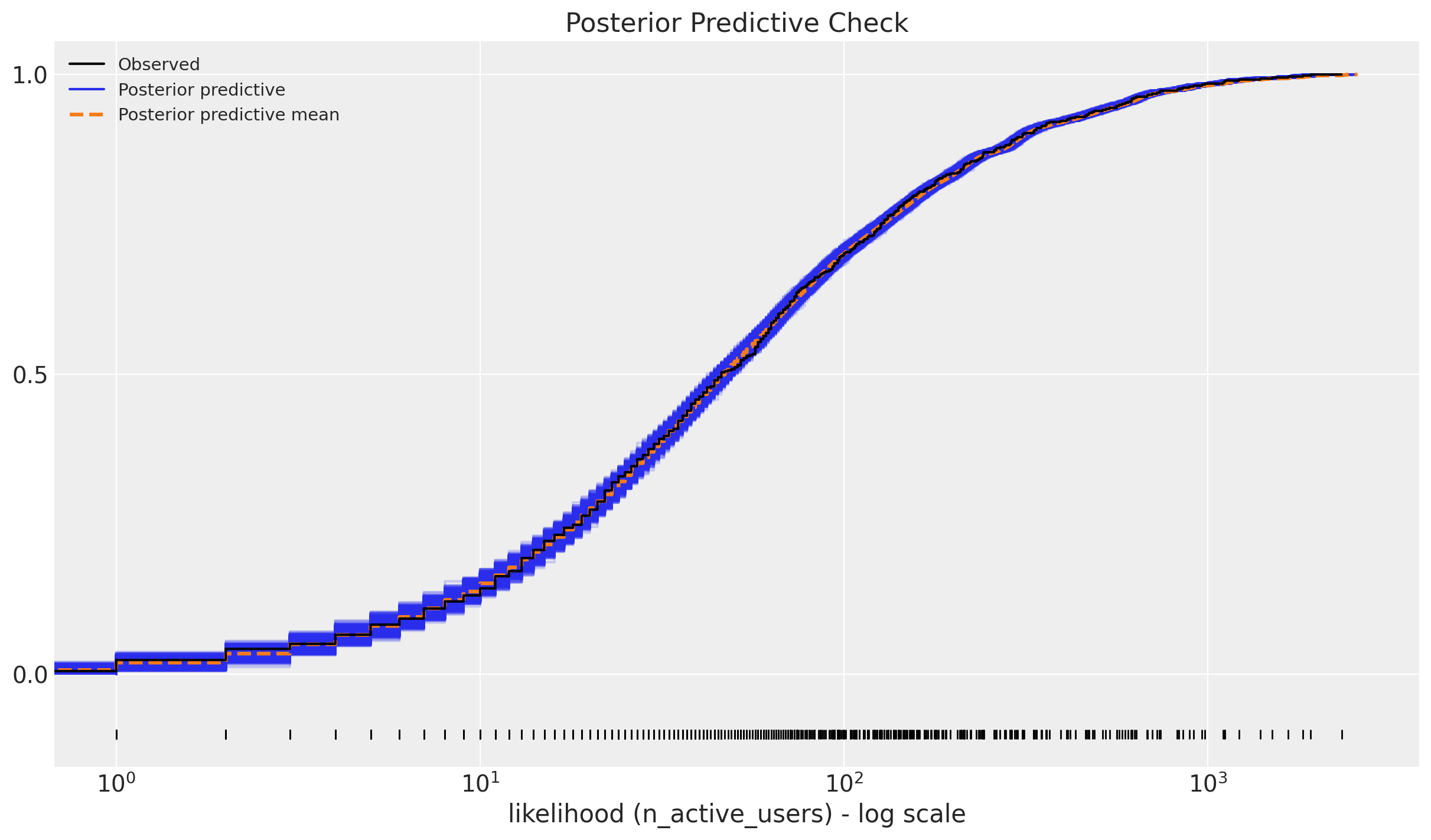
Posterior Predictive Check

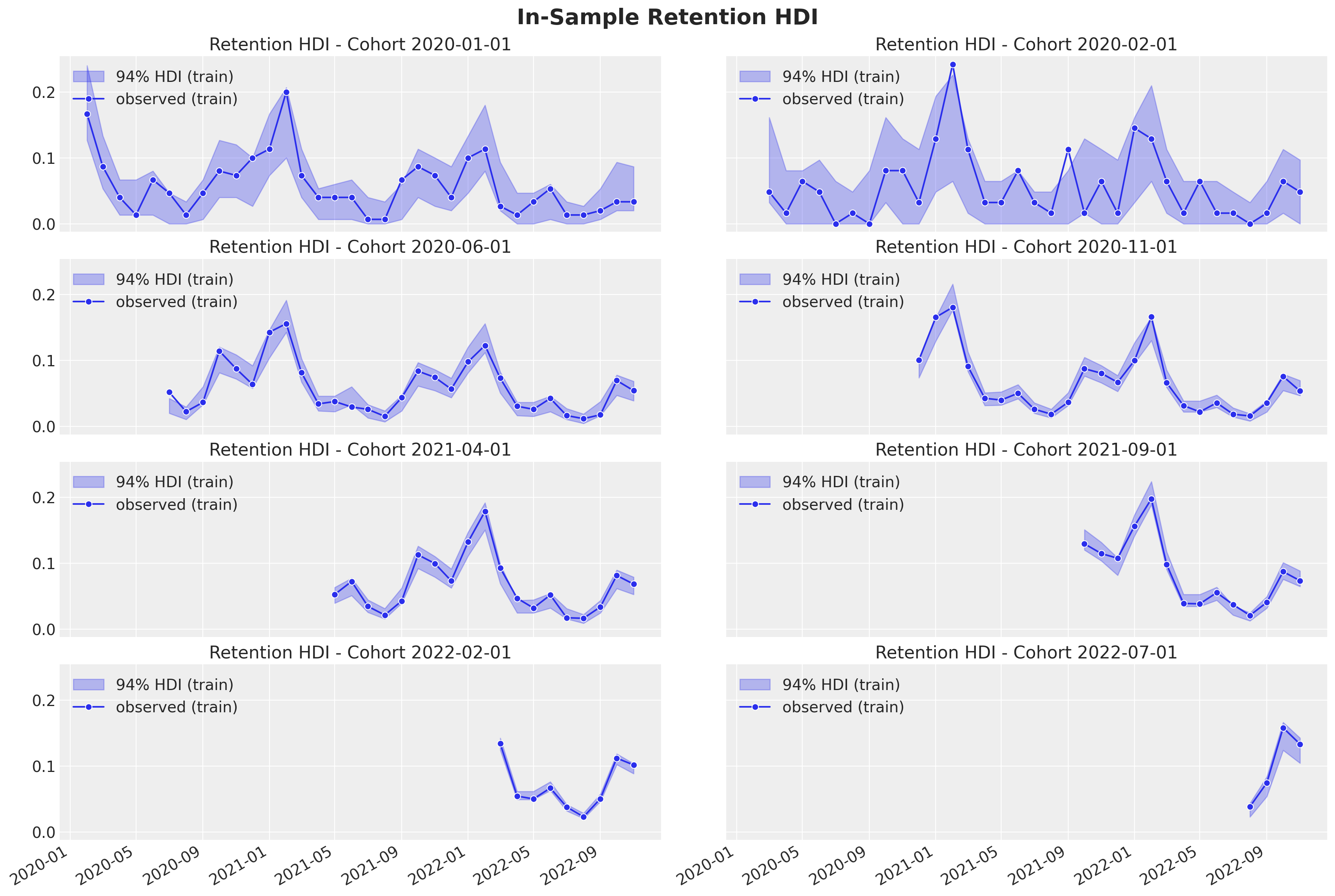
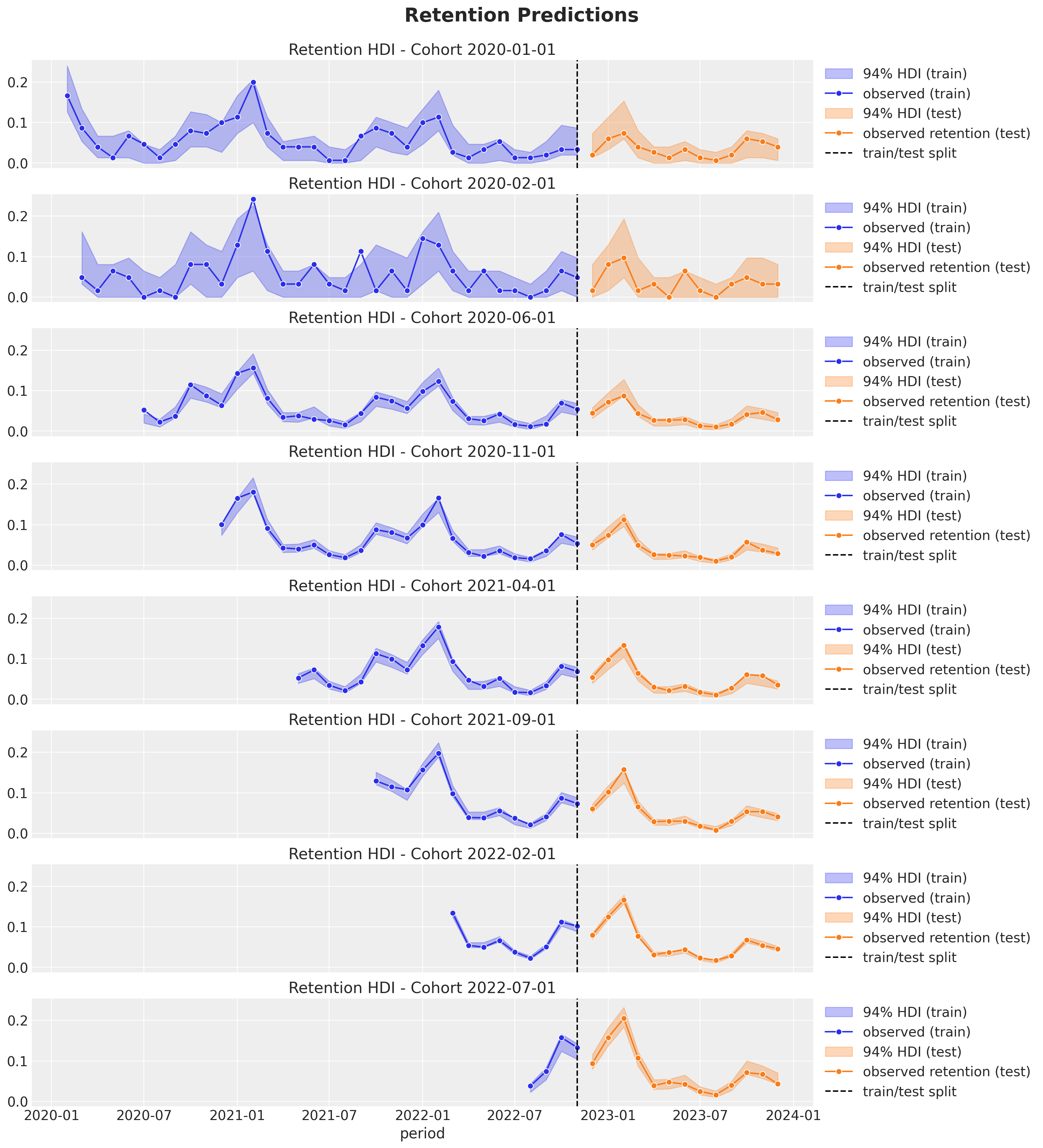
In-Sample Predictions

Out-of-Sample Predictions

More Complex Models - Requirements

• In many real-world scenarios, the data is more complex and the linear model is not enough. We need a more flexible model that can capture non-linearities and interactions.

• We care about uncertainty.

• We want to be able to iterate fast.

• Interested in out-of-sample predictions.

• We want to couple retention modeling with revenue modeling (CLV).

Bayesian Additive Regression Trees

• Bayesian “sum-of-trees” model where each tree is constrained by a regularization prior to be a weak learner.

• To fit the sum-of-trees model, BART uses PGBART, an inference algorithm based on the particle Gibbs method.

• BART depends on the number of trees \(m\in \mathbb{N}\) and prior parameters \(\alpha \in (0, 1)\) and \(\beta \in [0, \infty)\) so that the probability that a node at depth \(d \in \mathbb{N}_{0}\) is nonterminal is \(\alpha(1 + d)^{-\beta}\).

• BART is implemented in pymc-bart.

BART Retention Model

\[\begin{align*} N_{\text{active}} & \sim \text{Binomial}(N_{\text{total}}, p) \\ \textrm{logit}(p) & = \text{BART}(\text{cohort age}, \text{age}, \text{month}) \end{align*}\]

import pymc as pm
import pymc_bart as pmb

with pm.Model() as model
    ...
    mu = pmb.BART(
            name="mu",
            X=x,
            Y=train_retention_logit,
            m=100,
            response="mix",
            dims="obs",
        )
    ...

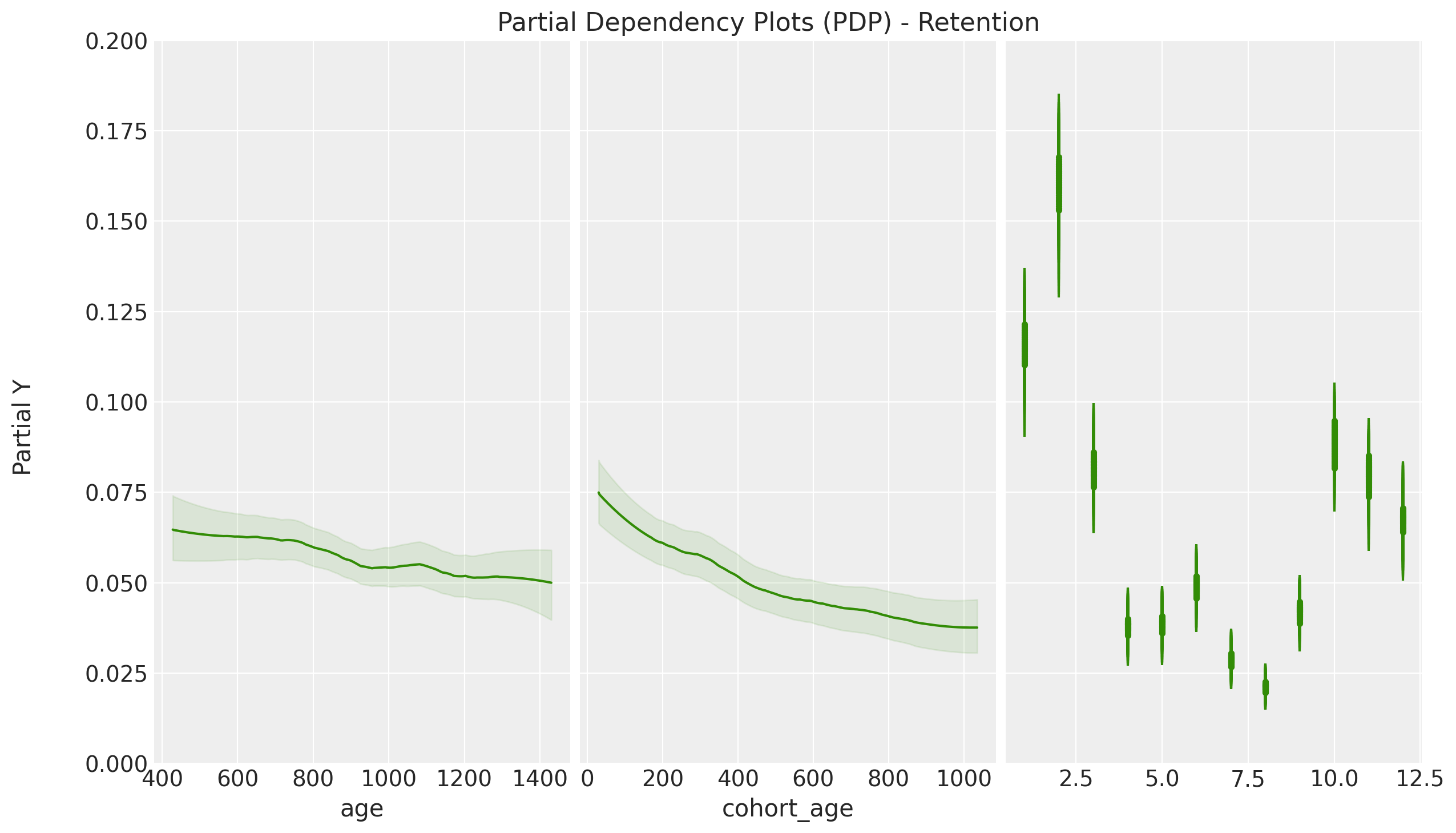
PDP Plot

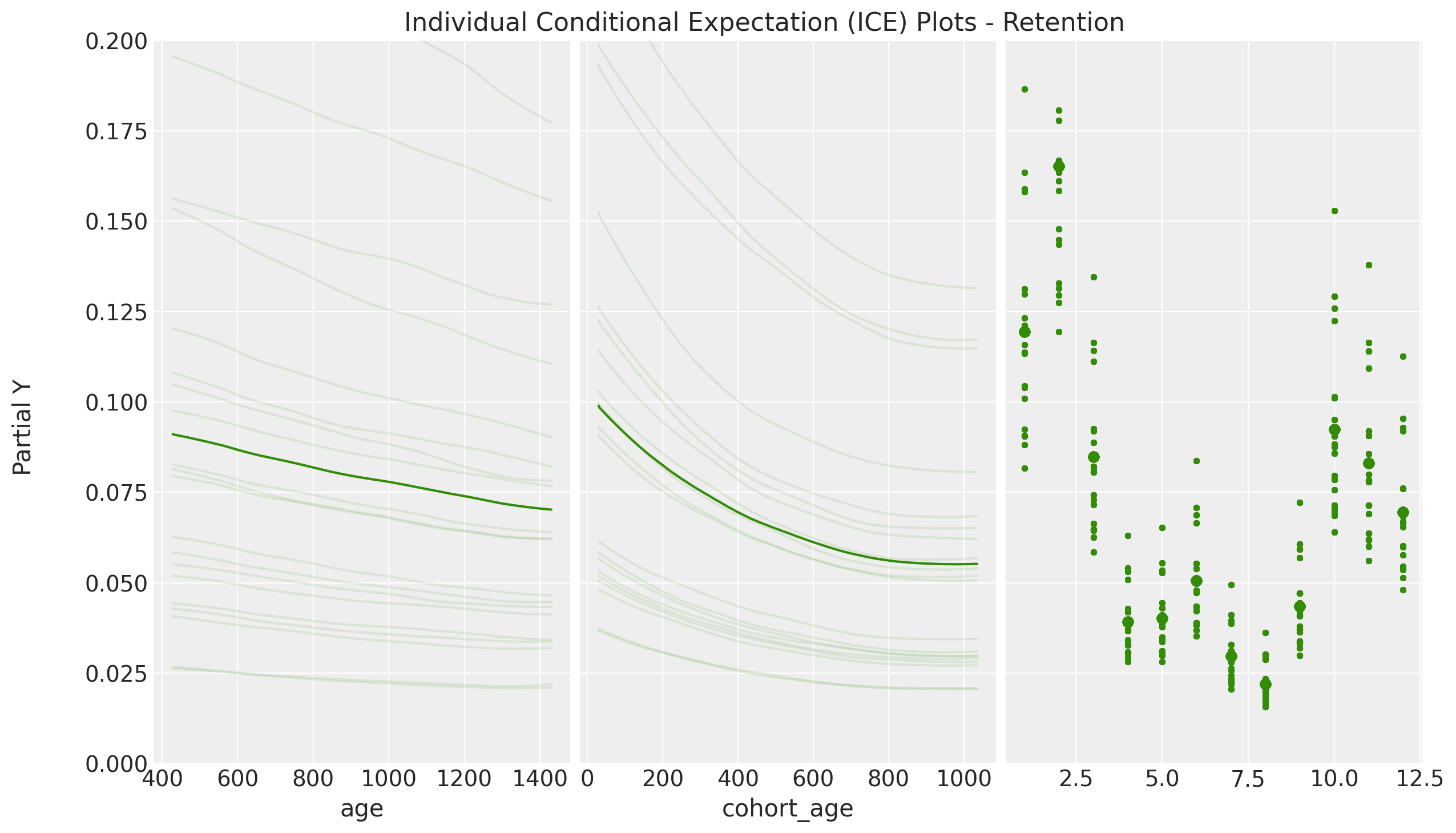
ICE Plot

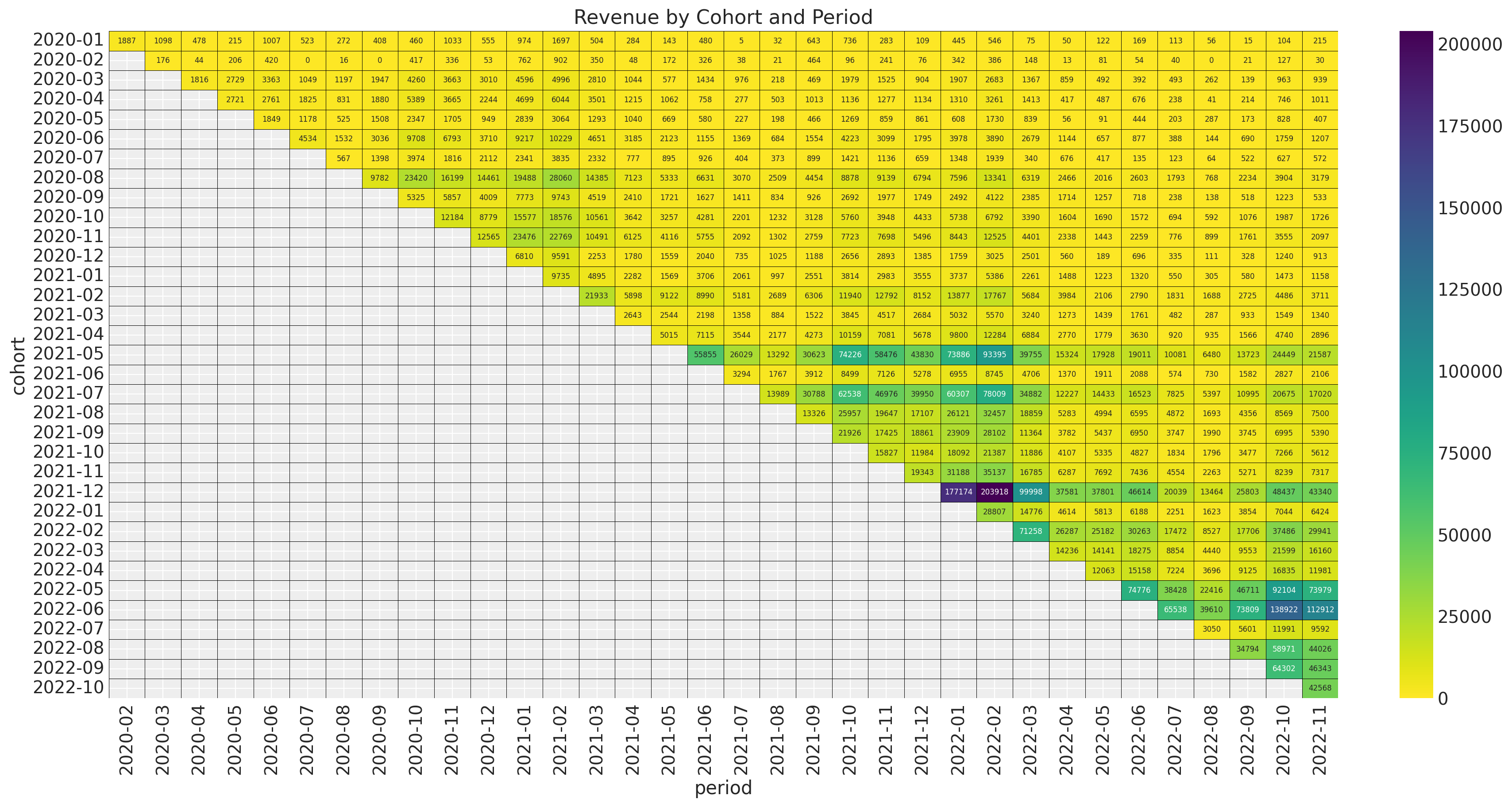
Revenue

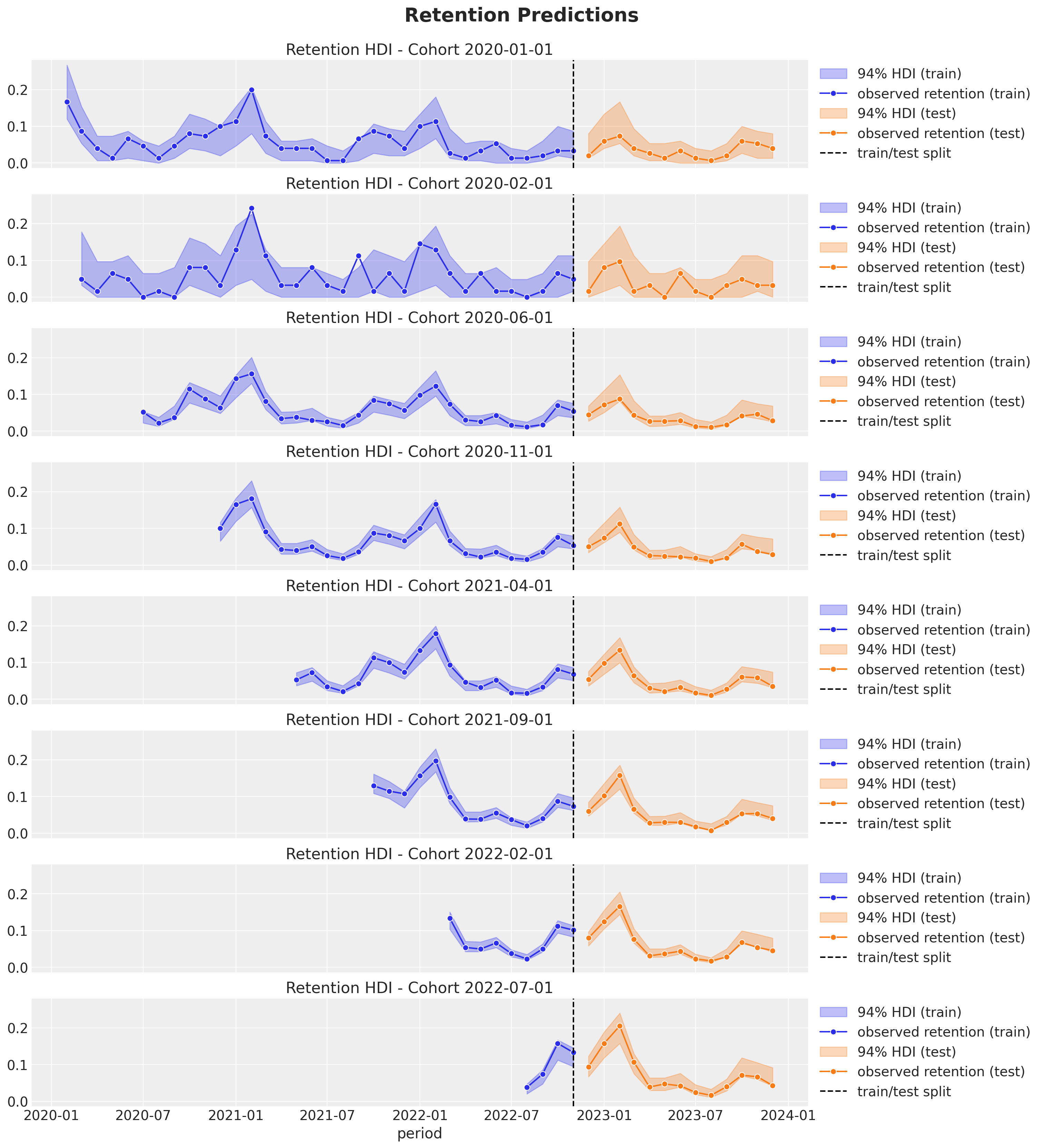
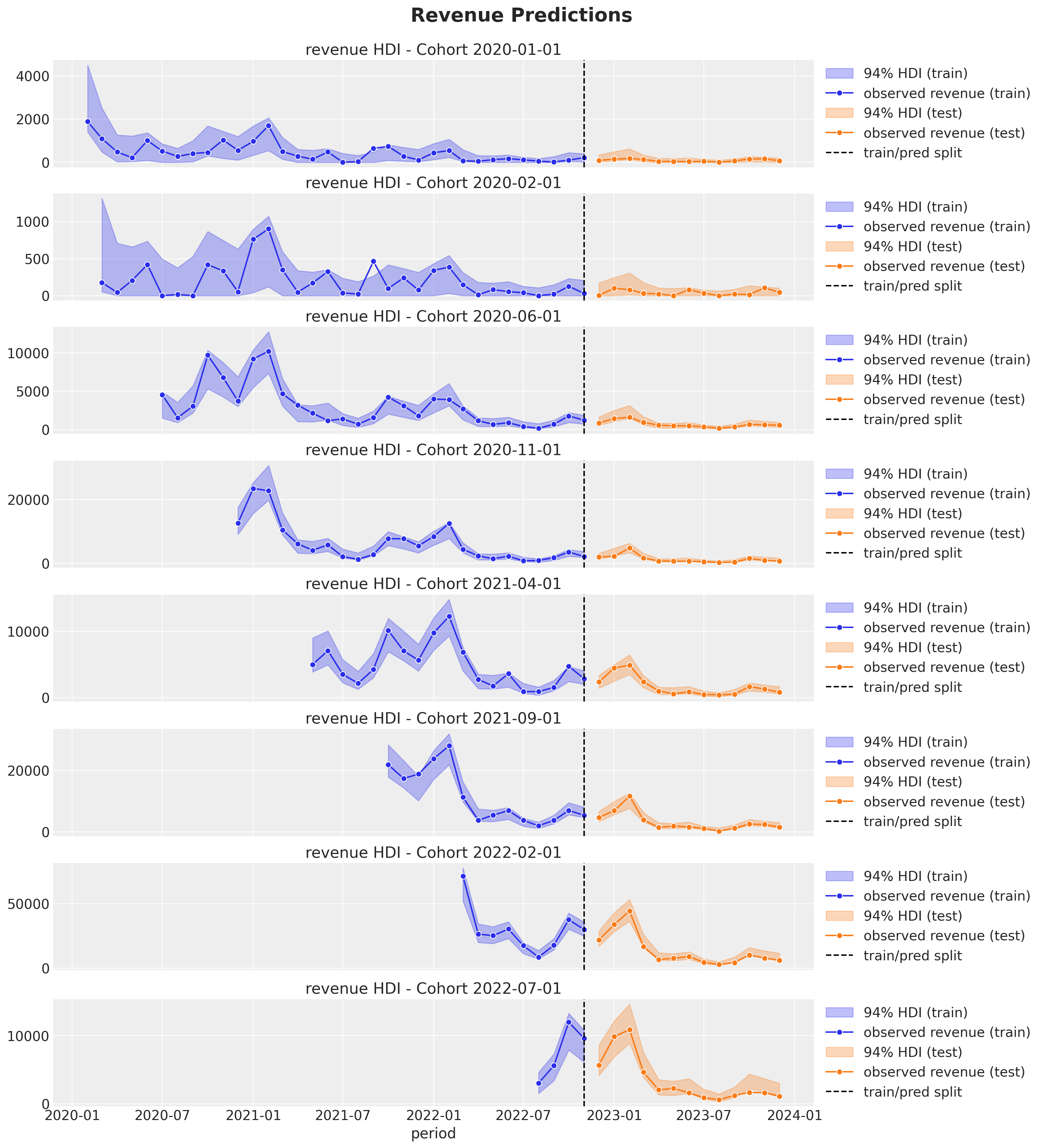
Cohort Revenue-Retention Model

%%{init: {"theme": "white", "themeVariables": {"fontSize": "48px"}, "flowchart":{"htmlLabels":false}}}%%
flowchart TD
  N[Number of Users] --> N_active[Number of Active Users]
  N_active --> Retention[Retention]
  Retention --> Revenue[Revenue]

Retention Component

\[\begin{align*} \textrm{logit}(p) & = \text{BART}(\text{cohort age}, \text{age}, \text{month}) \\ N_{\text{active}} & \sim \text{Binomial}(N_{\text{total}}, p) \end{align*}\]

Revenue Component

\[\begin{align*} \log(\lambda) = \: (& \text{intercept} \\ & + \beta_{\text{cohort age}} \text{cohort age} \\ & + \beta_{\text{age}} \text{age} \\ & + \beta_{\text{cohort age} \times \text{age}} \text{cohort age} \times \text{age}) \\ \text{Revenue} & \sim \text{Gamma}(N_{\text{active}}, \lambda) \end{align*}\]

Cohot Revenue-Retention Model

mu = pmb.BART(
    name="mu", X=x, Y=train_retention_logit, m=100, response="mix", dims="obs"
)

p = pm.Deterministic(name="p", var=pm.math.invlogit(mu), dims="obs")

lam_log = pm.Deterministic(
    name="lam_log",
    var=intercept
    + b_age_scaled * age_scaled
    + b_cohort_age_scaled * cohort_age_scaled
    + b_age_cohort_age_interaction * age_scaled * cohort_age_scaled,
    dims="obs",
)

lam = pm.Deterministic(name="lam", var=pm.math.exp(lam_log), dims="obs")

n_active_users_estimated = pm.Binomial(
    name="n_active_users_estimated",
    n=n_users,
    p=p,
    observed=n_active_users,
    dims="obs",
)

x = pm.Gamma(
    name="revenue_estimated",
    alpha=n_active_users_estimated + eps,
    beta=lam,
    observed=revenue,
    dims="obs",
)

Cohort Revenue-Retention Model

Revenue-Retention - Predictions

Some Applications in the Industry

• Understand retention and revenue drivers.

  • Factor out seasonality.

  • External covariates (e.g. acquisition channel).

• Forecast revenue and retention (cohort lifetime value).

• Causal Inference

  • Counterfactural analysis.

  • Geo experiments.

References

Blog Posts

• A Simple Cohort Retention Analysis in PyMC

• Cohort Retention Analysis with BART

• Cohort Revenue & Retention Analysis: A Bayesian Approach

Packages

• pymc
• pymc-bart

Papers

• BART: Bayesian additive regression trees
• Bayesian additive regression trees for probabilistic programming

References

Related Work

• Probability Models for Customer-Base Analysis

• “Counting Your Customers” the Easy Way: An Alternative to the Pareto/NBD Model, see pymc-marketing example here.

• BG/NBD Model in PyMC

• How to Project Customer Retention, see pymc-marketing example here.

• Fitting the sBG Model to Multi-Cohort Data

• Beta Survival Models

Open Source Packages

Thank you!

juanitorduz.github.io