Introduction to Hilbert Spaces Approximations Gaussian Processes

A conceptual and practical viewpoint

Dr. Juan Orduz

Outline

Reference Notebook 📓

https://juanitorduz.github.io/hsgp_intro/

  • 🐍 Reproducible Python Code (PyMC, Jax and NumPyro)
  • ✏️ Math and Code Examples

  1. Motivation: Some Applications

  2. Gaussian Processes

  3. Hilbert Space Approximation Deep Dive

  4. References

Motivation: Some Applications

Some Applications

How popular is the President?

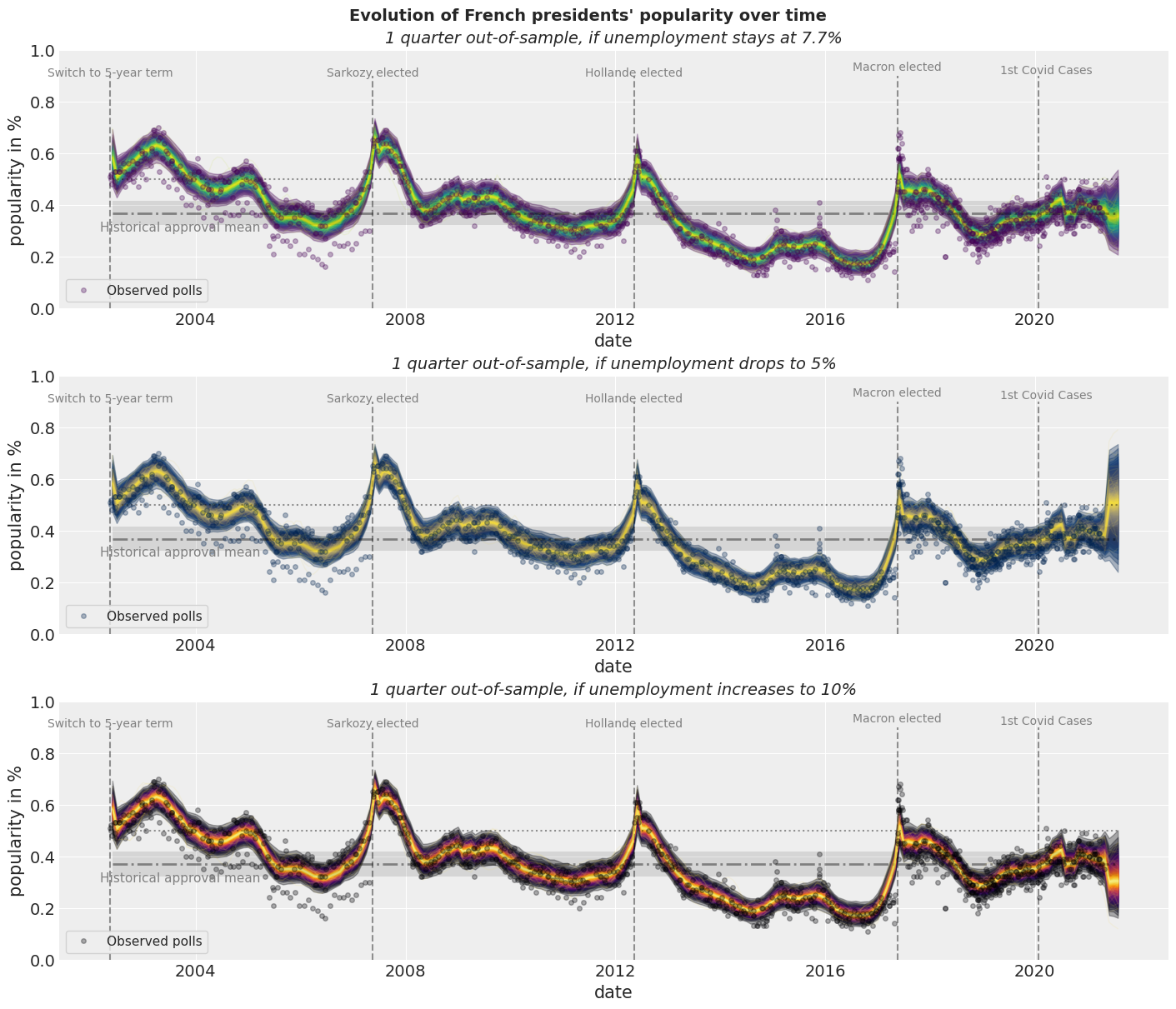
Some Applications

Time-Varying Regression Coefficients

Time-Varying Regression Coefficients via Hilbert Space Gaussian Process Approximation

Some Applications

Changes in marketing effectiveness over time

Bayesian Media Mix Models: Modelling changes in marketing effectiveness over time

Gaussian Processes

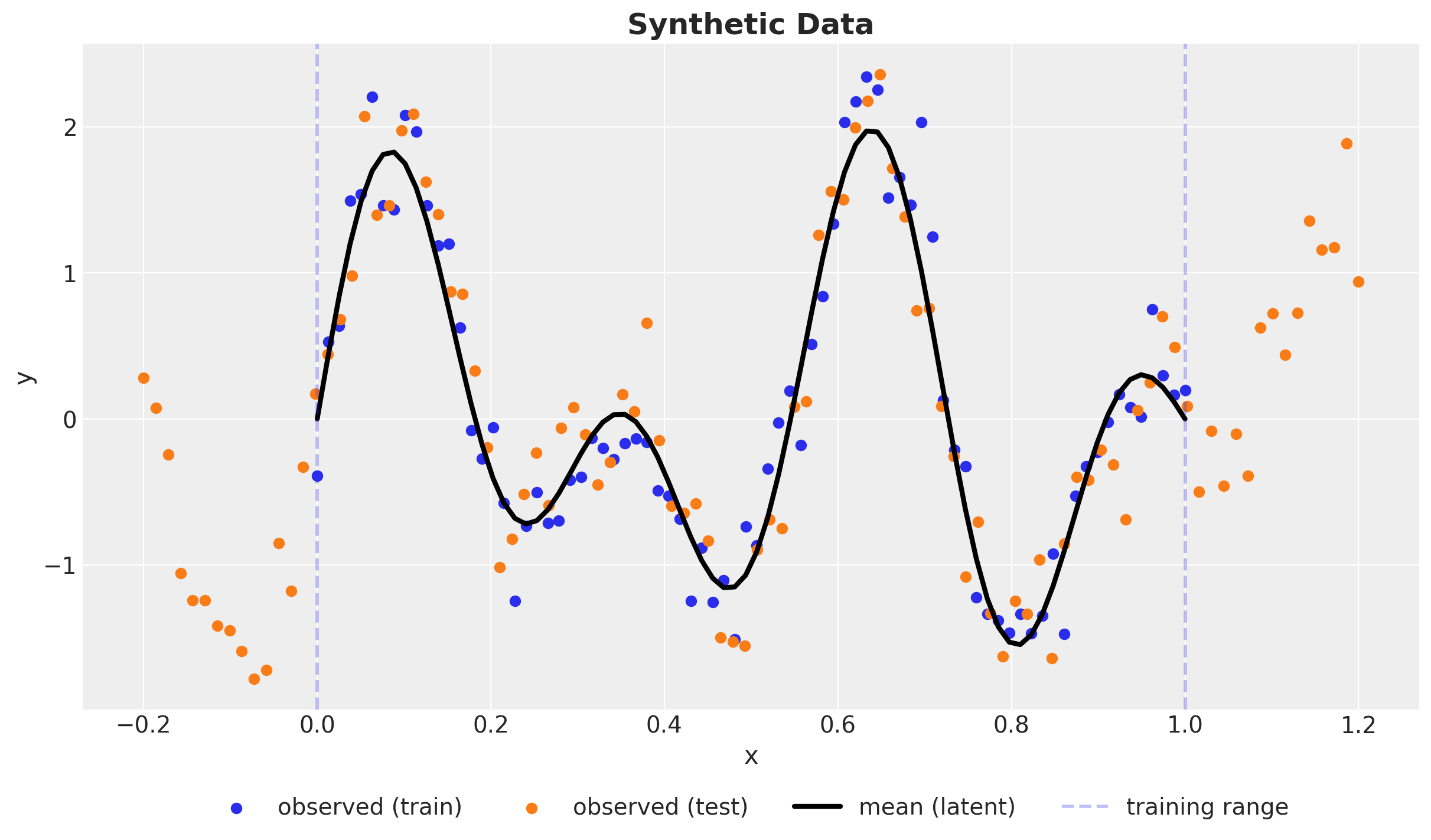
Synthetic Data

\(y \sim \text{Normal}(\sin(4 \pi x) + \sin(7 \pi x), 0.3^2)\)

Kernel

👉 A way to encode similarity between points.

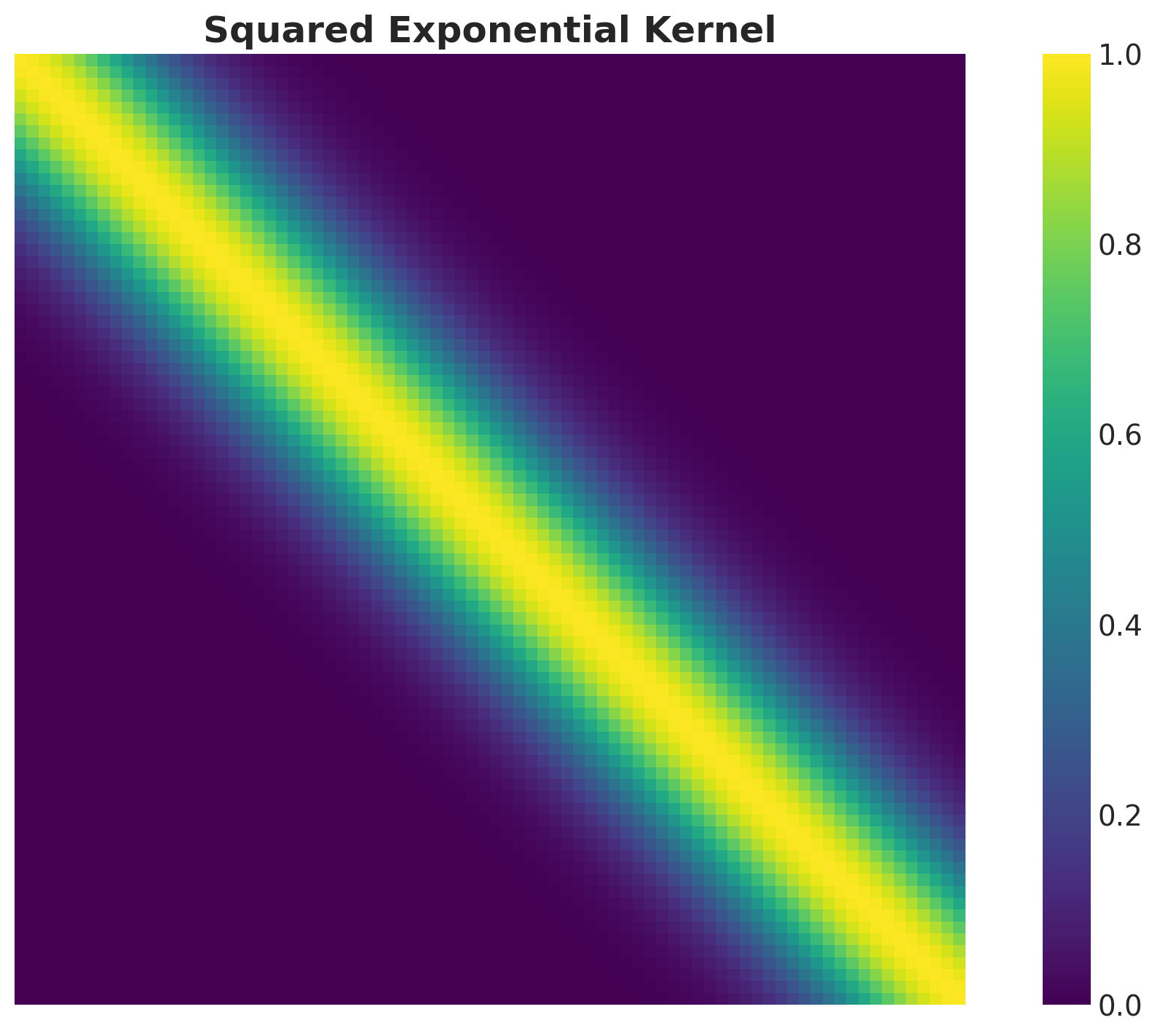
Example: Squared Exponential Kernel

\[ k(x, x') = a^ 2 \exp\left(-\frac{(x - x')^2}{2 \ell^2}\right) \]

Where \(a\) is the amplitude and \(\ell\) is the length-scale.

Note

Observe that the kernel just depends on the distance between points \(r = x - x'\). This is a property of stationary kernels.

Kernel Matrix

GP Model - Prior

Let us denote by \((x, y)\) and the training data and by \(x_{*}\) the test set for which we want to generate predictions. We define by \(f\) and \(f_*\) the latent functions for the training and test sets respectively.

\[ \left( \begin{array}{c} y \\ f_* \end{array} \right) \sim \text{MultivariateNormal}(0, \boldsymbol{K}) \]

where

\[ \boldsymbol{K} = \left( \begin{array}{cc} K(X, X) + \sigma^2_n I & K(X, X_*) \\ K(X_*, X) & K(X_*, X_*) \end{array} \right) \]

GP Model - Conditioning

\[ f_*|X, y, X_* \sim \text{MultivariateNormal}(\bar{f}_*, \text{cov}(f_*)) \]

where

\[ \begin{align*} \bar{f}_* &= K(X_*, X){\color{red}{(K(X, X) + \sigma^2_n I)^{-1}}} \\ \text{cov}(f_*) & = K(X_*, X_*) - K(X_*, X){\color{red}{(K(X, X) + \sigma^2_n I)^{-1}}} K(X, X_*) \end{align*} \]

Important

Taking the inverse of the kernel matrix is the most computationally expensive part of the GP model. It is of order \(\mathcal{O}(n^3)\).

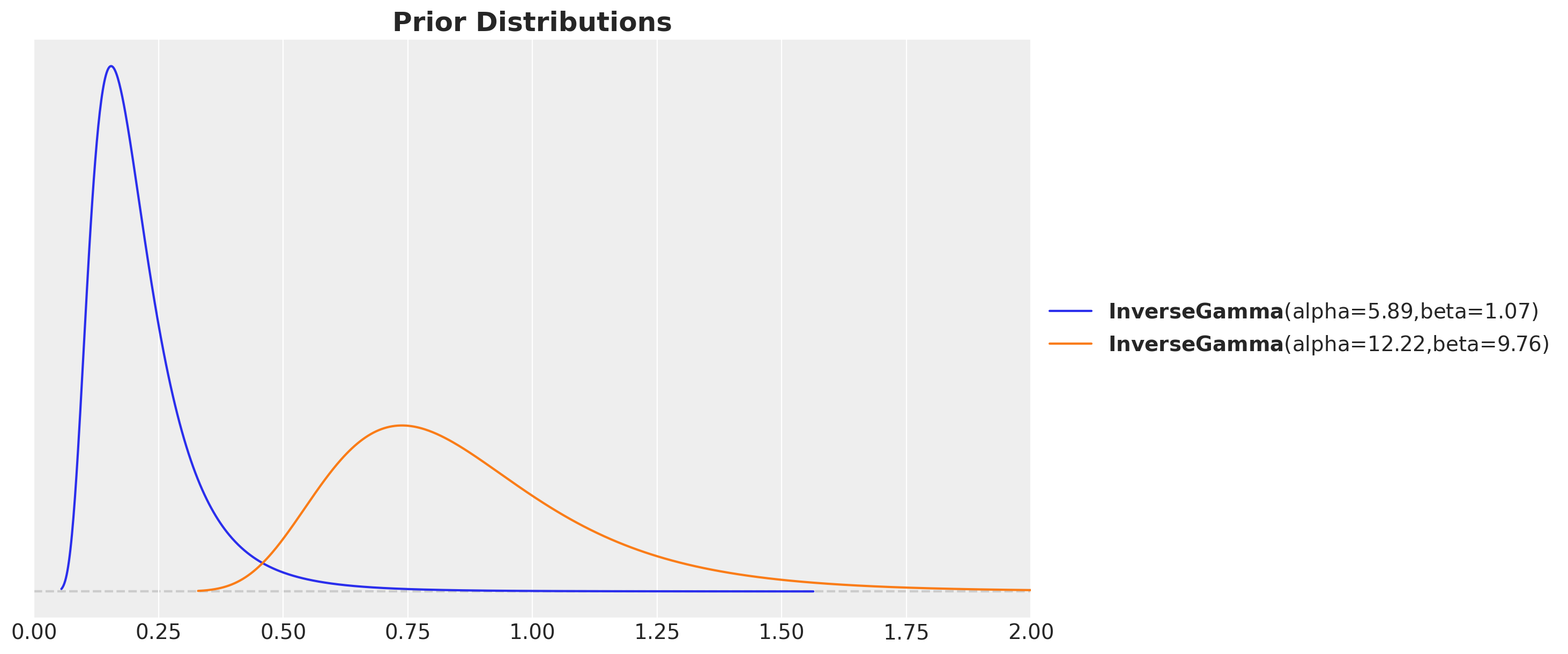
Kernel parameter priors

GP Model in PyMC

with pm.Model() as gp_pymc_model:
    x_data = pm.MutableData("x_data", value=x_train)

    kernel_amplitude = pm.InverseGamma("kernel_amplitude", ...)
    kernel_length_scale = pm.InverseGamma("kernel_length_scale", ...)
    noise = pm.InverseGamma("noise", ...)

    mean = pm.gp.mean.Zero()
    cov = kernel_amplitude**2 * pm.gp.cov.ExpQuad(
        input_dim=1, ls=kernel_length_scale
    )
    gp = pm.gp.Latent(mean_func=mean, cov_func=cov)
    f = gp.prior("f", X=x_data[:, None])

    pm.Normal("likelihood", mu=f, sigma=noise, observed=y_train_obs)

GP Model in PyMC

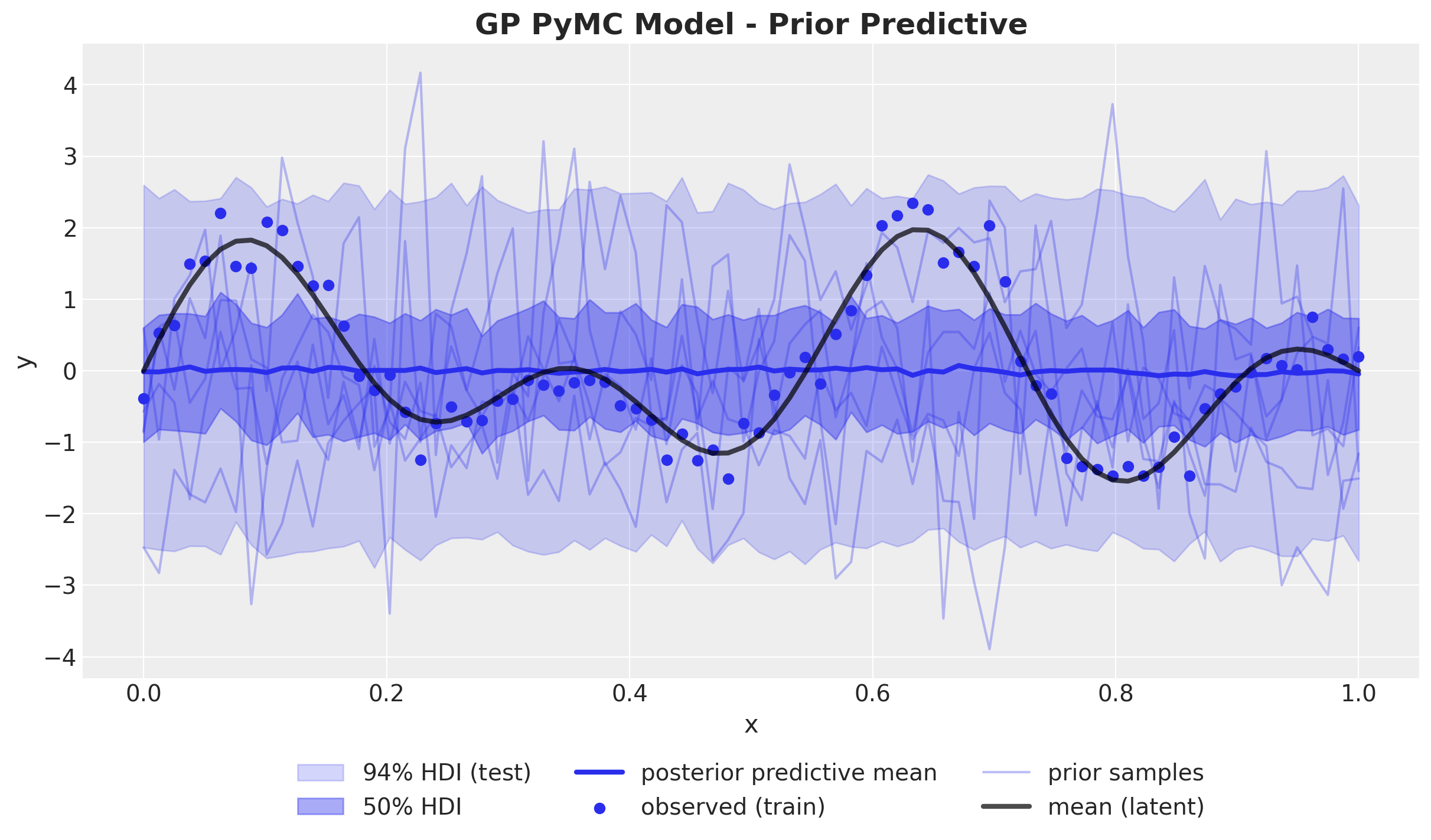
GP Model - Prior Predictions

GP Model - Posterior Distributions

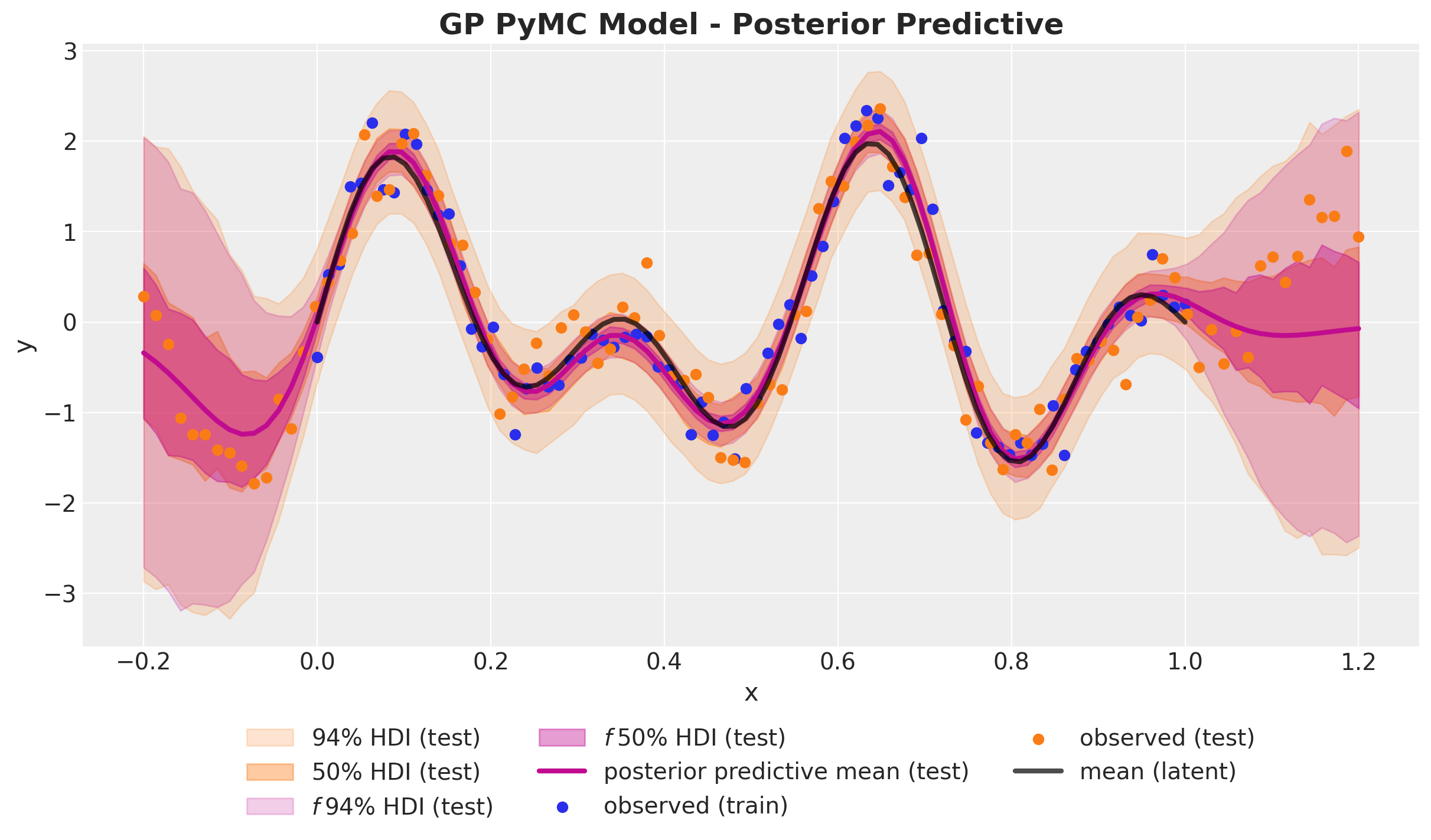
Out-of-Sample Predictions

conditional method

with gp_pymc_model:
    x_star_data = pm.MutableData("x_star_data", x_test)
    f_star = gp.conditional("f_star", x_star_data[:, None])
    pm.Normal("likelihood_test", mu=f_star, sigma=noise)

    gp_pymc_idata.extend(
        pm.sample_posterior_predictive(
            trace=gp_pymc_idata,
            var_names=["f_star", "likelihood_test"],
            random_seed=rng_subkey[1].item(),
        )
    )

GP Model - Posterior Predictive

Hilbert Space Gaussian Process (HSGP) Approximation

HSGP Deep Dive

Problem with scaling Gaussian processes?

👉 Inverting the kernel matrix is computationally expensive!

Approach Summary 🤓

  • Strategy: Approximate the kernel matrix \(K\) with a a matrix with a smaller rank.

  • Key Idea: Interpret the covariance function as the kernel of a pseudo-differential operator and approximate it using Hilbert space methods.

  • Result: A reduced-rank approximation where the basis functions are independent of the covariance functions and their parameters (plus asymptotic convergence).

Hilbert space methods for reduced-rank Gaussian process regression

Hilbert Space Approximation

%%{init: {"theme": "white", "themeVariables": {"fontSize": "54px"}, "flowchart":{"htmlLabels": false}}}%%
flowchart TD
  kernel["kernel"] --> spectral_density["Spectral Density"]
  spectral_density --> polynomial["Polynomial Expansion"]
  laplacian["Laplacian"] --> fourier["Fourier Transform"]
  laplacian --> dirichlet["Dirichlet's BC"]
  dirichlet --> spectral_decomposition["Spectral Decomposition"]
  spectral_decomposition["Spectral Decomposition"] --> functional["Functional Calculus"]
  polynomial --> identify_coefficients["Identify Coefficients"]
  fourier --> identify_coefficients
  functional --> identify_coefficients
  identify_coefficients --> approximation["Approximation Formula"]

style kernel fill:#2a2eec80
style laplacian fill:#fa7c1780
style approximation fill:#328c0680
style fourier fill:#c10c9080
style spectral_decomposition fill:#65e5f380

Hilbert Space Approximation - Steps

  1. D-Tour: Eigenvalues and Eigenvectors.
  2. We recall the spectral density \(S(\omega)\) associated with a stationary kernel function \(k\).
  3. We approximate the spectral density \(S(\omega)\) as a polynomial series in \(||\omega||^2\).
  4. We can interpret these polynomial terms as powers of the Laplacian operator. The key observation is that the Fourier transform of the Laplacian operator is \(||\omega||^2\).
  5. Next, we impose Dirichlet boundary conditions on the Laplacian operator which makes it self-adjoint and with a discrete spectrum.
  6. We identify the expansion in (2) with the sum of powers of the Laplacian operator in the eigenbasis of (4).
  7. We arrive at the final approximation formula and explicitly compute the terms for the squared exponential kernel in the one-dimensional case.

\[ f(x) \approx \sum_{j = 1}^{m} \overbrace{\underbrace{\color{red}{\left(S(\sqrt{\lambda_j})\right)^{1/2}}}_{\text{All hyperparameters are here!}}}^{\text{Spectral density evaluated at the eigenvalues}} \times \overbrace{\underbrace{\color{blue}{\phi_{j}(x)}}_{\text{Easy to compute!}}}^{\text{Laplacian Eigenfunctions}} \times \overbrace{\color{green}{\beta_{j}}}^{\sim \: \text{Normal}(0,1)} \]

Eigenvalues and Eigenvectors

Recall that given a matrix \(A\) (or a linear operator) the eigenvalues and eigenvectors are the solutions to the equation

\[A v = \lambda v\]

where \(v \neq \vec{0}\) is the eigenvector and \(\lambda\) is the eigenvalue.

The spectrum of a matrix is the set of its eigenvalues.

The Spectral Theorem for Matrices

Example - \(2 \times 2\) Matrix

\[ A = \begin{pmatrix} 1 & 2 \\ 2 & 1 \end{pmatrix} \]

The eigenvalues are \(\lambda_1 = 3\) and \(\lambda_2 = -1\) with eigenvectors:

\[ v_1 = \frac{1}{\sqrt{2}} \begin{pmatrix} 1 \\ 1 \end{pmatrix} \quad \text{and} \quad v_2 = \frac{1}{\sqrt{2}} \begin{pmatrix} -1 \\ 1 \end{pmatrix} \]

Orthonormal Basis

\[ v_1^{T} v_2 = 0 \quad \text{and} \quad v_1^{T} v_1 = v_2^{T} v_2 = 1 \]

The Spectral Theorem

The spectral theorem states that we can always find such orthonormal basis of eigenvectors for a symmetric matrix.

Change of Basis

Observe that if we consider the change-of-basis matrix

\[ Q = \begin{pmatrix} v_1 & v_2 \end{pmatrix} \]

then we can write the matrix \(A\) in the new basis as

\[ D = Q^{T} A Q = \begin{pmatrix} 3 & 0 \\ 0 & -1 \end{pmatrix} \]

Code Example

import jax.numpy as jnp

A = jnp.array([[1.0, 2.0], [2.0, 1.0]])

# Compute eigenvalues and eigenvectors
eigenvalues, eigenvectors = jnp.linalg.eig(A)

print(f"Eigenvalues: {eigenvalues}\nEigenvectors:\n{eigenvectors}")

>> Eigenvalues: [ 3.+0.j -1.+0.j]
>> Eigenvectors:
>> [[ 0.70710678+0.j -0.70710678+0.j]
>> [ 0.70710678+0.j  0.70710678+0.j]]


# Change of basis matrix
Q = eigenvectors
Q.T @ A @ Q

>> Array([[ 3.00000000e+00+0.j,  4.44089210e-16+0.j],
       [ 6.10622664e-16+0.j, -1.00000000e+00+0.j]], dtype=complex128)

The Spectral Theorem for Matrices

Spectral Projections

\[ A = \sum_{j=1}^{2} \color{red}{\lambda_i} \color{blue}{v_j v_j^{T}} \]

The operator \(P_{j} = v_j v_j ^{T}\) satisfies \(P^2 = P\) and \(P^T = P\).

def proj(v, x):
    return jnp.dot(v, x) * v

def matrix_proj(x):
    return eigenvalues[0] * proj(Q[:, 0], x) + eigenvalues[1] * proj(Q[:, 1], x)

# Arbitrary vector
v = jnp.array([1.0, 2.0])
jnp.allclose(jnp.dot(A, v), matrix_proj(v))
>> Array(True, dtype=bool)

Functional Calculus

The functional calculus is a generalization of the Taylor series for functions to operators. Given a function \(f\) we can define the operator \(f(A)\) as

\[ f(A) = \sum_{j=1}^{2} \color{red}{f(\lambda_j)} \color{blue}{v_j v_j^{T}} \]

Examples

  • \(f(z) = z\) we recover the operator \(A\).
  • \(f(z) = 1\) we get the identity operator \(I\).
  • \(f(z) = z^2\) we get the operator \(A^2\).
  • \(f(z) =e^{z}\) we get the operator \(\exp(A)\).

Spectral Densities

In the case a kernel function is stationary, we can use the spectral representation of the kernel function (Bochner’s theorem) and write it as:

\[ k(r) = \frac{1}{(2 \pi)^{d}}\int_{\mathbb{R}^{d}} e^{i \omega^{T} r} {\color{red}{S(\omega)}} d\omega \]

where \(\color{red}{S(\omega)}\) is the spectral density corresponding to the covariance function.

Gaussian Processes for Machine Learning - Chapter 4: Covariance Functions.

(Here we are assuming the positive measure from Bochner’s theorem has a density, i.e. \(d\mu(\omega) = S(\omega)d\omega\))

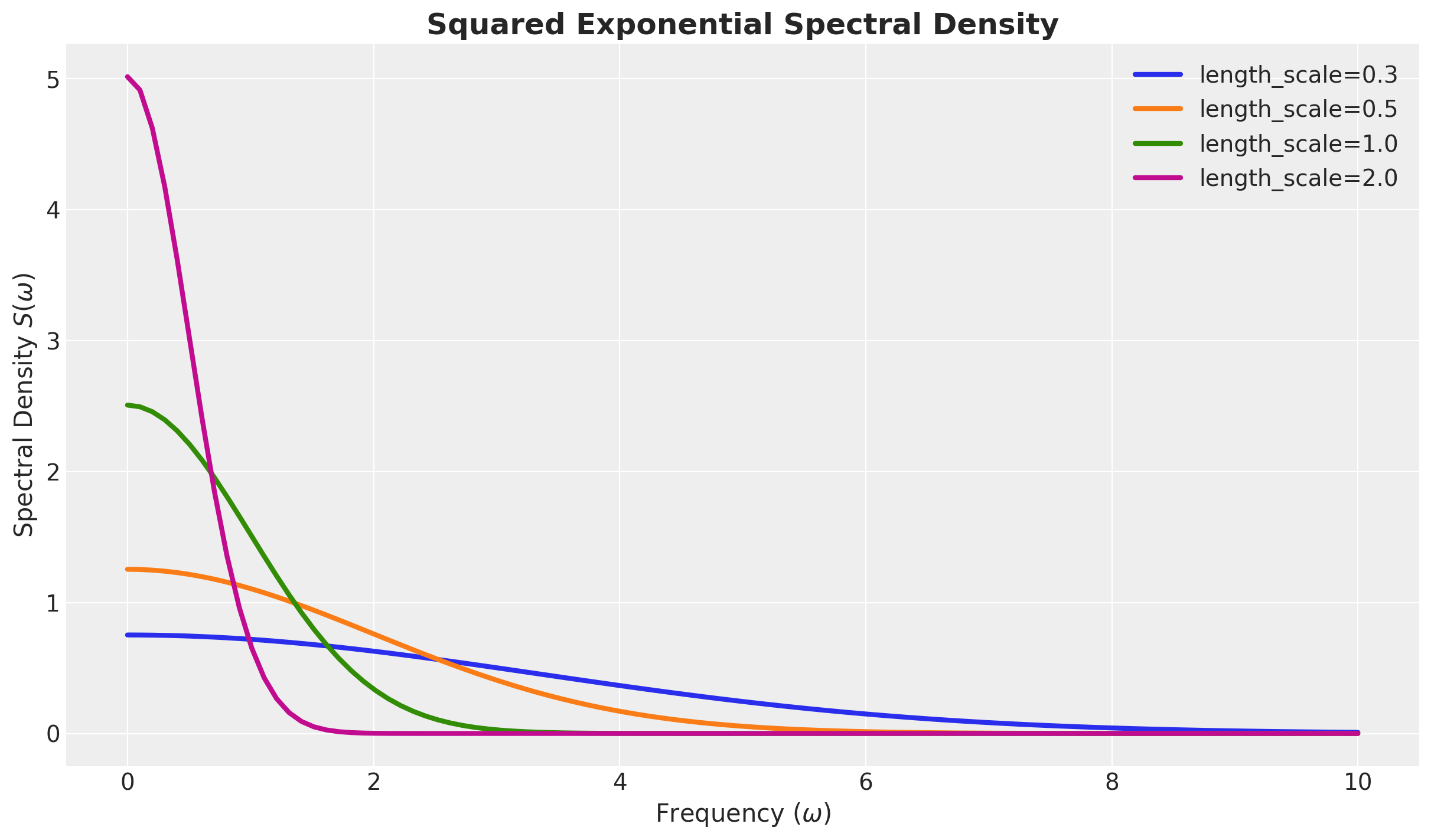
Spectral Density - Example

For the squared exponential kernel, it can be shown that

\[ S(\omega) = a^2(2 \pi \ell^2)^{d/2} \exp\left(-2\pi^2\ell^2\omega^2\right) \]

# d = 1
def squared_exponential_spectral_density(w, amplitude, length_scale):
    c = amplitude**2 * jnp.sqrt(2 * jnp.pi) * length_scale
    e = jnp.exp(-0.5 * (length_scale**2) * (w**2))
    return c * e

Note the similarity between the spectral density and the Fourier transform. For Gaussian-like kernels, like the squared exponential, we expect the associated spectral density to also be Gaussian-like.

\(S(\omega)\) Squared Exponential

Formal Power Expansion of the Spectral Density

Let us assume the kernel function is isotropic, i.e. it just depends on the Euclidean norm \(||r||\).

  • \(S(\omega)\) is also isotropic.

  • Write \(S(||\omega||) = \psi(||\omega||^2)\) for a suitable function \(\psi\).

  • We can expand \(\psi\) (Taylor-like expansion)

    \[ \begin{align*} \psi(||\omega||^2) = a_0 + a_1 (||\omega||^2) + a_2 (||\omega||^2)^2 + a_3 (||\omega||^2)^3 + \cdots \end{align*} \]

The Laplace Operator

Recall the Laplace operator is defined as

\[ - \nabla^2 f = \sum_{i=1}^{d} \frac{\partial^2 f}{\partial x_i^2} \]

Properties

The Laplacian has many good properties:

  • Positive semi-definite

  • Elliptic

  • Self-adjoint (appropriate boundary conditions)*

Unbounded Self-adjoint Operators on Hilbert Space

Kernel as a function of \(\nabla^2\)

One can verify that the Fourier transform of the Laplacian is

\[ \mathcal{F}[\nabla^2 f](\omega) = - ||\omega||^2 \mathcal{F}[f] \]

Formal expansion as powers of the Laplacian

We can write the integral operator associated with the kernel

\[ \mathcal{K} := \int_{\mathbb{R}^d} k(\cdot, x')f(x') dx' \]

as

\[ \mathcal{K} = a_0 + a_1 (- \nabla^2) + a_2 (-\nabla^2)^2 - a_3 (-\nabla^2)^3 + \cdots \]

Dirichlet’s Laplacian - Spectrum

Dirichlet boundary conditions: Only consider function vanishes on the boundary of the domain \(\Omega\).

  • It is is a self-adjoint operator defined on the Hilbert space \(L^{2}(\Omega)\) equipped with the Lebesgue measure. That is,

    \[ \int_{\Omega} {\color{purple}{(-\nabla^2 f(x))}} g(x) dx = \int_{\Omega} f(x) {\color{purple}{(-\nabla^2 g(x))}} dx \]

  • It has discrete spectrum with eigenvalues \({\color{red}{\lambda_j}} \rightarrow \infty\) and eigenfunctions \(\color{blue}{\phi_j}\) that form an orthonormal basis of \(L^2(\Omega)\)

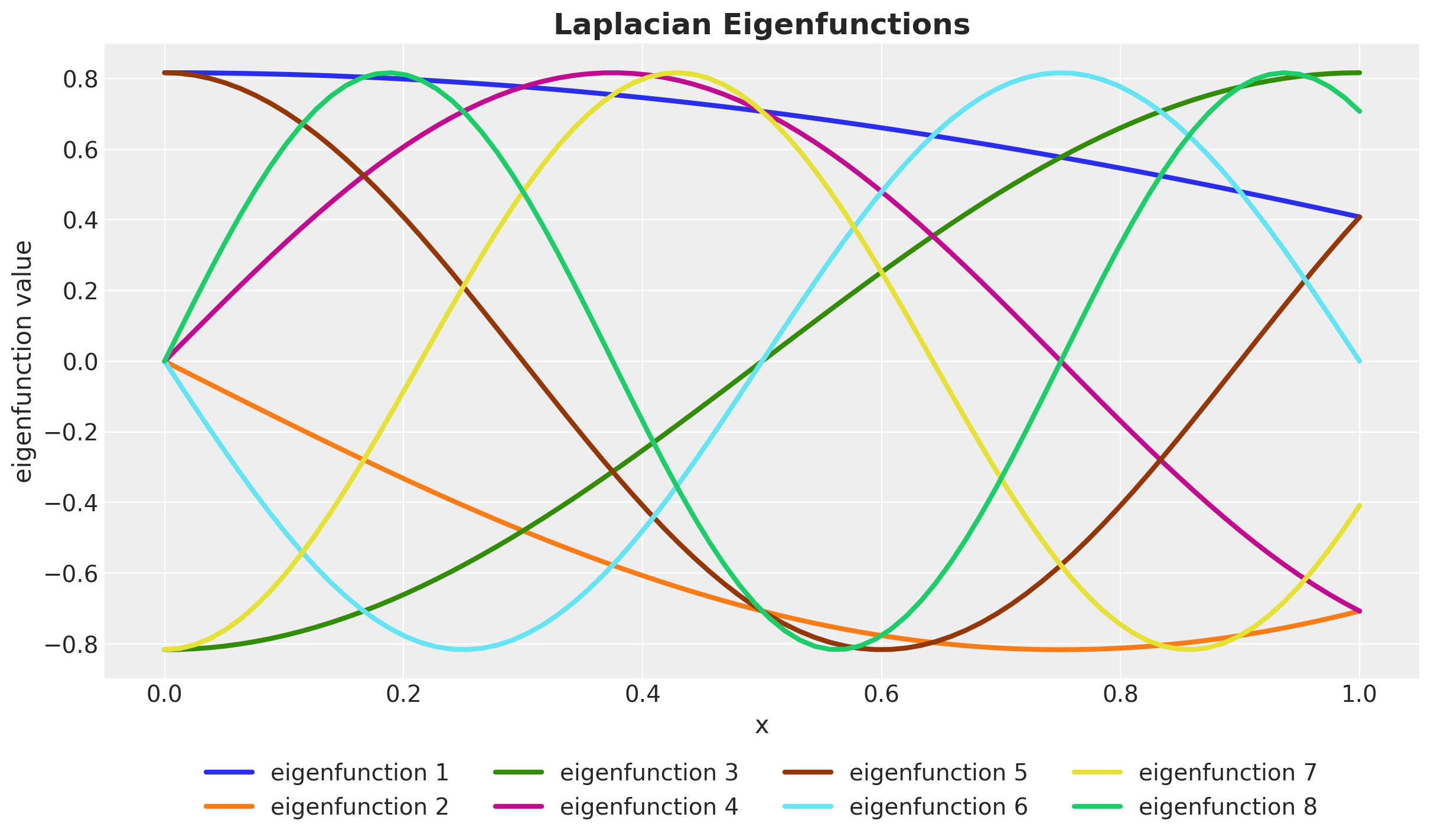
Unbounded Self-adjoint Operators on Hilbert Space

Example - \(\Omega = [-L, L] \subset \mathbb{R}\)

\[ \frac{d^2 \phi}{dx^2} = - \lambda \phi \quad \text{with} \quad \phi(-L) = \phi(L) = 0 \]

Spectrum

\[ \phi_j(x) = \sqrt{\frac{1}{L}} \sin\left(\frac{\pi j (x + L)}{2L}\right) \quad \text{and} \quad \lambda_j = \left(\frac{j \pi}{2L}\right)^2 \quad \text{for} \: j = 1, 2, \ldots \]

def laplace_eigenfunctions(x, l_max: float, m: int):
    sqrt_eigenvalues = laplacian_sqrt_eigenvalues(l_max, m)
    rep_x = jnp.tile(l_max + x[:, None], reps=m)
    diag_sqrt_eigenvalues = jnp.diag(sqrt_eigenvalues)
    num = jnp.sin(rep_x @ diag_sqrt_eigenvalues)
    den = jnp.sqrt(l_max)
    return num / den

Laplace Eigenfunctions

HSGP: Functional Calculus

\[ -\nabla^2 f(x) = \int_{\Omega} \overbrace{\left[\sum_{j} \lambda_{j} \phi_{j}(x) \phi_{j}(x')\right]}^{l(x, x')} f(x') dx' \]

We can construct powers of \(-\nabla^2\) as

\[ (- \nabla^2)^{s} f(x) = \int_{\Omega} {\color{red}{\overbrace{\left[\sum_{j} \lambda_{j}^{s} \phi_{j}(x) \phi_{j}(x')\right]}^{l^s(x, x')}}} f(x') dx'. \]

HSGP: Coefficients Identification

\[ \begin{align*} & \overbrace{\left[ a_{0} + a_{1}(-\nabla^2) + a_{2}(-\nabla^2)^2 + \cdots \right]}^{\mathbfcal{K}}f(x) = \\ &\int_{\Omega} \left[a_{0} + a_{1} l(x, x') + a_{2} l^{2}(x, x') + \cdots \right] f(x') dx' \end{align*} \]

This implies we can approximate the kernel as

\[ \begin{align*} k(x, x') \approx & \: a_{0} + a_{1} l(x, x') + a_{2} l^{2}(x, x') + \cdots \\ \approx & \sum_{j} {\color{red}{\underbrace{\left[ a_{0} + a_{1} \lambda_{j} + a_{2} \lambda_{j}^2 + \cdots \right]}_{S(\sqrt{\lambda_{j}})}}} \phi_{j}(x) \phi_{j}(x') \end{align*} \]

HSGP: Final Formula

In summary, we have the following approximation formula for the kernel function:

\[ \boxed{ k(x, x') \approx \sum_{j}^{m} \color{red}{S(\sqrt{\lambda_j})}\color{blue}{\phi_{j}(x) \phi_{j}(x')} } \]

That is, the model of the Gaussian process \(f\) can be written as

\[ f(x) \sim \text{MultivariateNormal}(\boldsymbol{\mu}, \Phi\mathcal{D}\Phi^{T}) \]

where \(\mathcal{D} = \text{diag}(S(\sqrt{\lambda_1}), S(\sqrt{\lambda_2}), \ldots, S(\sqrt{\lambda_{m}}))\).

HSGP: Linear Model

\[ f(x) \approx \sum_{j = 1}^{m} \overbrace{\color{red}{\left(S(\sqrt{\lambda_j})\right)^{1/2}}}^{\text{all hyperparameters are here!}} \times \underbrace{\color{blue}{\phi_{j}(x)}}_{\text{easy to compute!}} \times \overbrace{\color{green}{\beta_{j}}}^{\sim \: \text{Normal}(0,1)} \]

Key Observations

  • The only dependence on the hyperparameters is through the spectral density.

  • The computational cost of evaluating the log posterior density of univariate HSGPs scales as \(\mathcal{O}(nm + m)\).

Squared Exponential \(1\)-dim

\[ \begin{align*} k(x, x') \approx \sum_{j=1}^{m} & \color{red}{\overbrace{\left(a^2 \sqrt{2 \pi} \ell \exp\left(-2\pi^2\ell^2 \left(\frac{\pi j}{2L}\right)^2 \right)\right)^{1/2}}^{\left(S(\sqrt{\lambda_j})\right)^{1/2}}} \\ & \times \color{blue}{\overbrace{\left(\sqrt{\frac{1}{L}} \sin\left(\frac{\pi j (x + L)}{2L}\right)\right)}^{\phi_{j}(x)}} \\ & \times \color{green}{\overbrace{\beta_{j}}^{\sim \: \text{Normal}(0, 1)}} \end{align*} \]

Hilbert Space Approximation (Recap)

%%{init: {"theme": "white", "themeVariables": {"fontSize": "54px"}, "flowchart":{"htmlLabels": false}}}%%
flowchart TD
  kernel["kernel"] --> spectral_density["Spectral Density"]
  spectral_density --> polynomial["Polynomial Expansion"]
  laplacian["Laplacian"] --> fourier["Fourier Transform"]
  laplacian --> dirichlet["Dirichlet's BC"]
  dirichlet --> spectral_decomposition["Spectral Decomposition"]
  spectral_decomposition["Spectral Decomposition"] --> functional["Functional Calculus"]
  polynomial --> identify_coefficients["Identify Coefficients"]
  fourier --> identify_coefficients
  functional --> identify_coefficients
  identify_coefficients --> approximation["Approximation Formula"]

style kernel fill:#2a2eec80
style laplacian fill:#fa7c1780
style approximation fill:#328c0680
style fourier fill:#c10c9080
style spectral_decomposition fill:#65e5f380

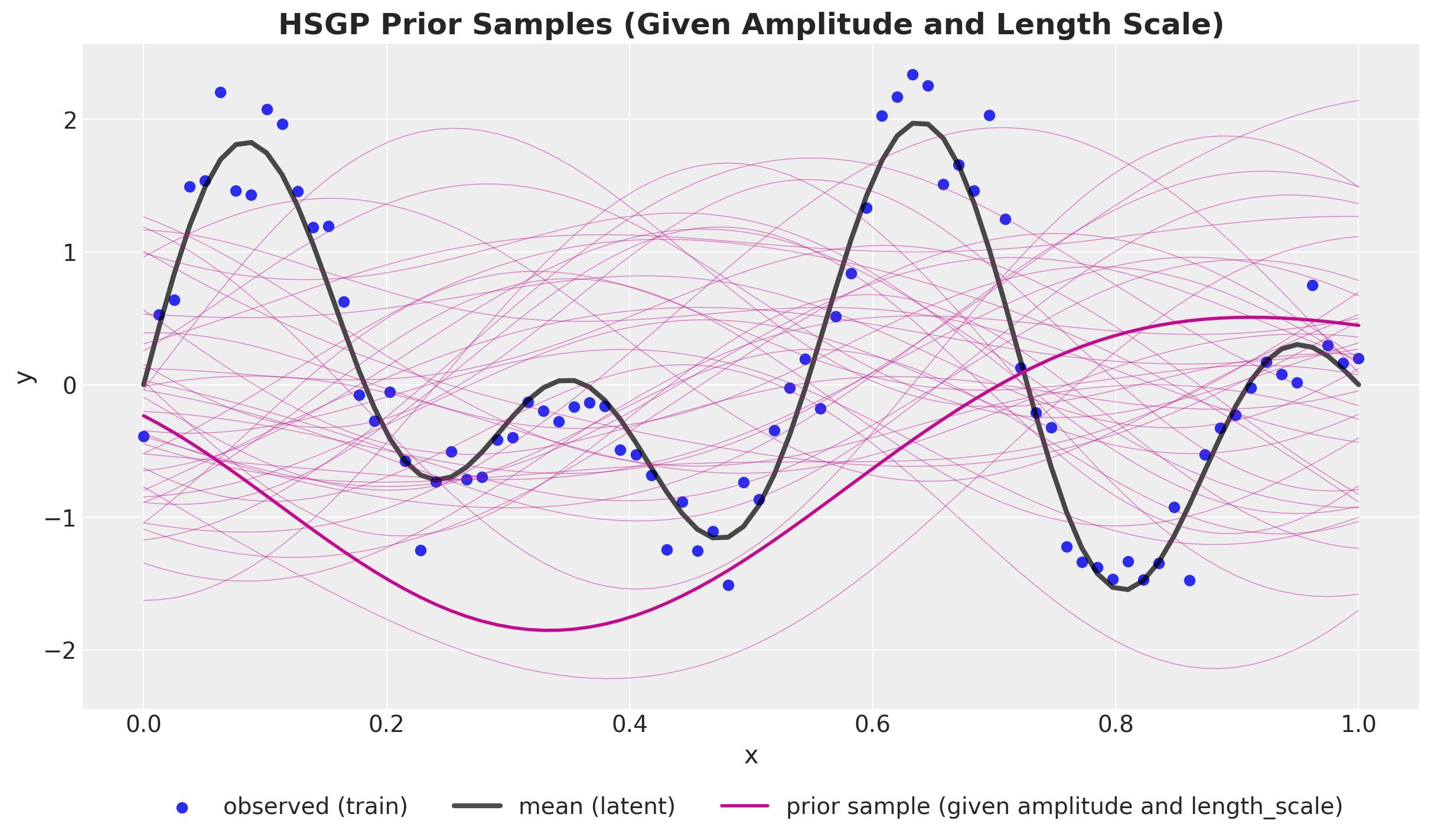
Prior Predictive

NumPyro Implementation

def hs_approx_squared_exponential_ncp(x, amplitude, length_scale, l_max, m):
    phi = laplace_eigenfunctions(x, l_max, m)
    spd = jnp.sqrt(
        diag_squared_exponential_spectral_density(amplitude, length_scale, l_max, m)
    )
    with numpyro.plate("basis", m):
        beta = numpyro.sample("beta", dist.Normal(0, 1))
    return numpyro.deterministic("f", phi @ (spd * beta))


def hsgp_model(x, l_max, m, y=None) -> None:
    # --- Priors ---
    kernel_amplitude = numpyro.sample("kernel_amplitude", ...)
    kernel_length_scale = numpyro.sample( "kernel_length_scale", ...)
    noise = numpyro.sample( "noise", ...)
    # --- Parametrization ---
    f = hs_approx_squared_exponential_ncp(
        x, kernel_amplitude, kernel_length_scale, l_max, m
    )
    # --- Likelihood ---
    with numpyro.plate("data", x.shape[0]):
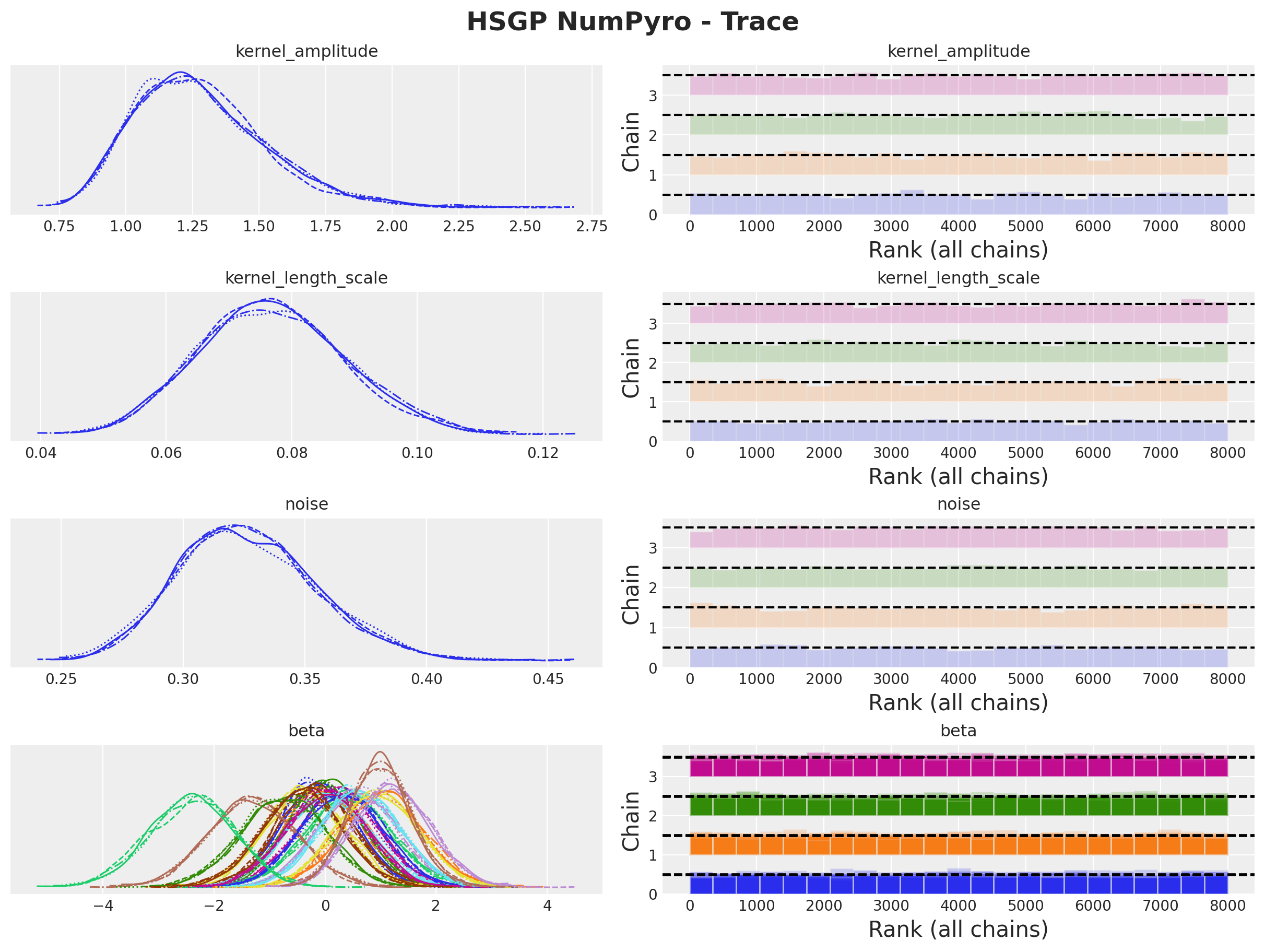
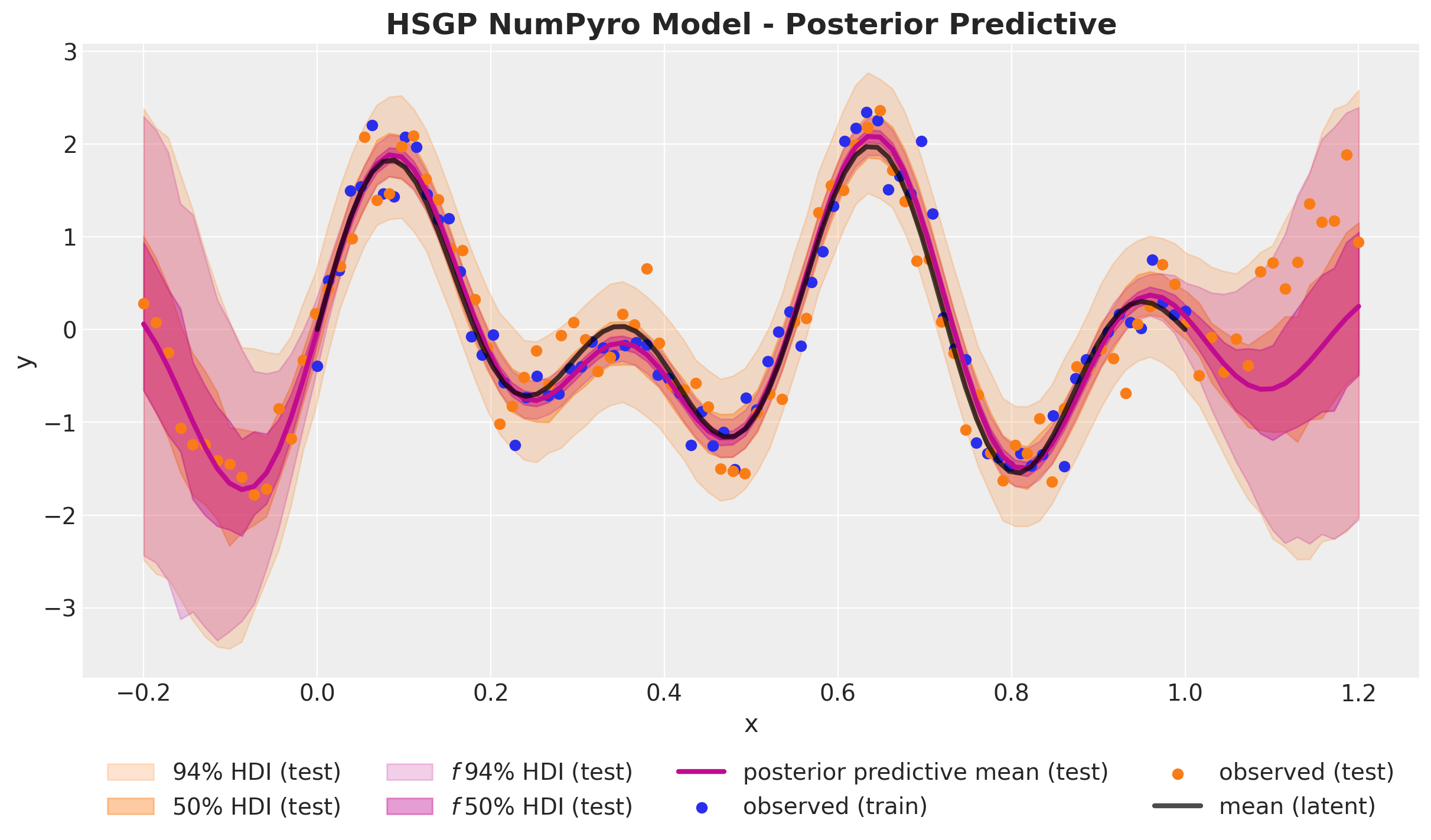
        numpyro.sample("likelihood", dist.Normal(loc=f, scale=noise), obs=y)

HSGP Model - Posterior

HSGP Model - Posterior Predictive

PyMC Implementation

HSGP Class

with pm.Model() as hsgp_pymc_model:
    x_data = pm.MutableData("x_data", value=x_train)
    y_data = pm.MutableData("y_data", y_train_obs)

    kernel_amplitude = pm.InverseGamma("kernel_amplitude", ...)
    kernel_length_scale = pm.InverseGamma("kernel_length_scale", ...)
    noise = pm.InverseGamma("noise", ...)

    mean = pm.gp.mean.Zero()
    cov = kernel_amplitude**2 * pm.gp.cov.ExpQuad(
        input_dim=1, ls=kernel_length_scale
    )
    gp = pm.gp.HSGP(m=[20], L=[1.3], mean_func=mean, cov_func=cov)
    f = gp.prior("f", X=x_data[:, None])

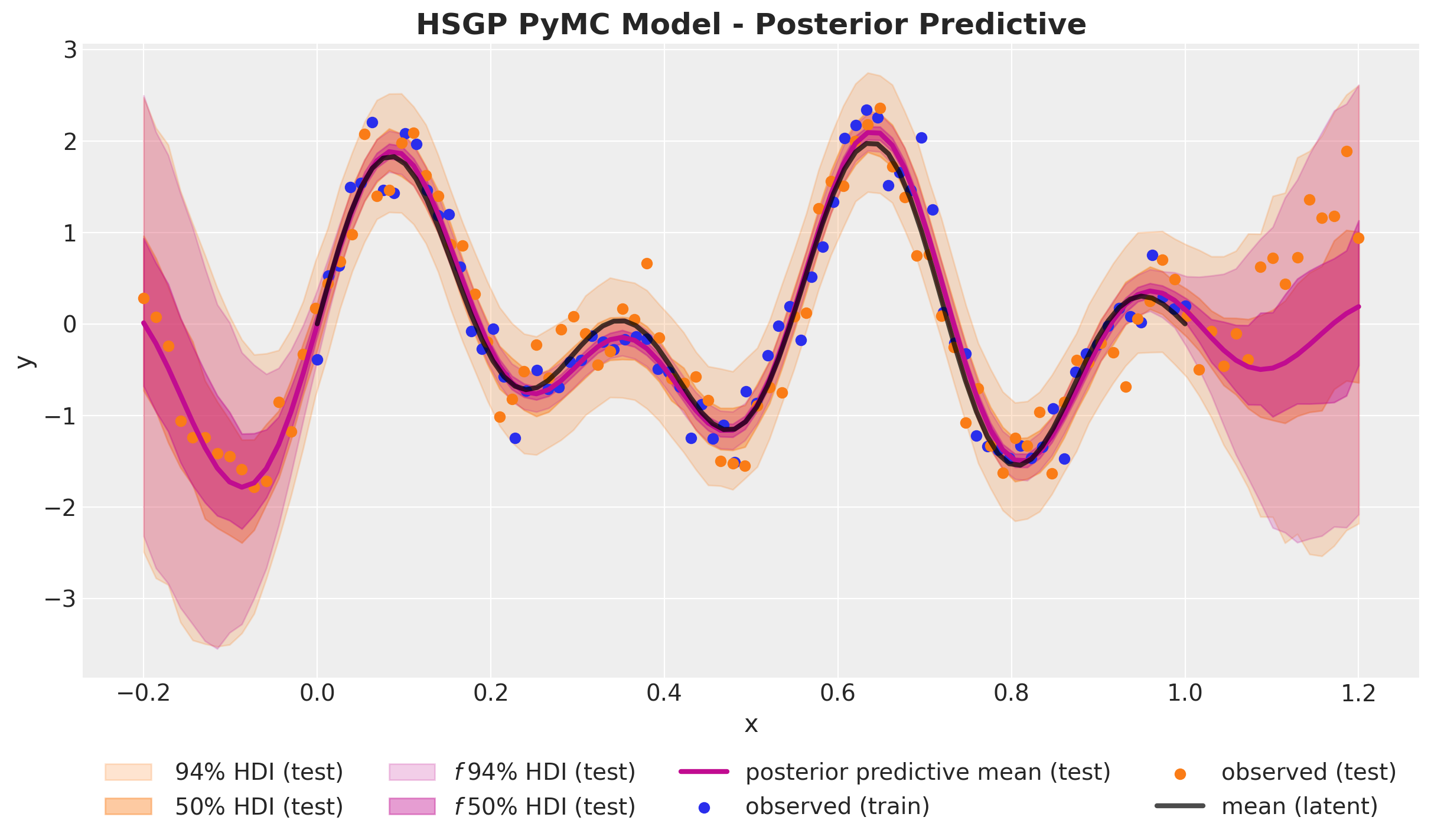
    pm.Normal("likelihood", mu=f, sigma=noise, observed=y_data)

Out-of-Sample Predictions

conditional method

with hsgp_pymc_model:
    x_star_data = pm.MutableData("x_star_data", x_test)
    f_star = gp.conditional("f_star", x_star_data[:, None])
    pm.set_data({"x_data": x_test, "y_data": np.ones_like(x_test)})
    hsgp_pymc_idata.extend(
        pm.sample_posterior_predictive(
            trace=hsgp_pymc_idata,
            var_names=["f_star", "likelihood"],
            random_seed=rng_subkey[1].item(),
        )
    )

HSGP Model - Posterior Predictive

PyMC Implementation

HSGP.prior_linearized

with pm.Model() as hsgp_linearized_pymc_model:
    x_data = pm.MutableData("x_data", value=x_train)
    y_data = pm.MutableData("y_data", y_train_obs)

    kernel_amplitude = pm.InverseGamma("kernel_amplitude", ...)
    kernel_length_scale = pm.InverseGamma("kernel_length_scale", ...)
    noise = pm.InverseGamma("noise", ...)

    mean = pm.gp.mean.Zero()
    cov = kernel_amplitude**2 * pm.gp.cov.ExpQuad(input_dim=1, ls=kernel_length_scale)
    gp = pm.gp.HSGP(m=[20], L=[1.3], mean_func=mean, cov_func=cov)
    phi, sqrt_psd = gp.prior_linearized(Xs=x_data_centered[:, None])

    beta = pm.Normal("beta", mu=0, sigma=1, size=gp._m_star)
    f = pm.Deterministic("f", phi @ (beta * sqrt_psd))

    pm.Normal("likelihood", mu=f, sigma=noise, observed=y_data)

Out-of-Sample Predictions

pm.set_data method

with hsgp_pymc_model:
    pm.set_data({"x_data": x_test, "y_data": np.ones_like(x_test)})
    hsgp_linearized_pymc_idata.extend(
        pm.sample_posterior_predictive(
            trace=hsgp_pymc_idata,
            var_names=[
                "f",
                "likelihood",
            ],
            random_seed=rng_subkey[1].item(),
        )
    )

References

Gaussian Processes

HSGP Approximation

References

Birthdays Dataset

Spectral Theory

Thank you!

juanitorduz.github.io