Introduction to Hilbert Spaces Approximations Gaussian Processes

A conceptual and practical viewpoint

Dr. Juan Orduz

Mathematician & Data Scientist

Outline

Reference Notebook 📓

https://juanitorduz.github.io/hsgp_intro/

  • 🐍 Reproducible Python Code (PyMC, Jax and NumPyro)
  • ✏️ Math and Code Examples

  1. Motivation: Some Applications

  2. Gaussian Processes

  3. Hilbert Space Approximation Deep Dive

  4. Example: Birthdays Dataset

  5. References

Motivation: Some Applications

Some Applications

How popular is the President?

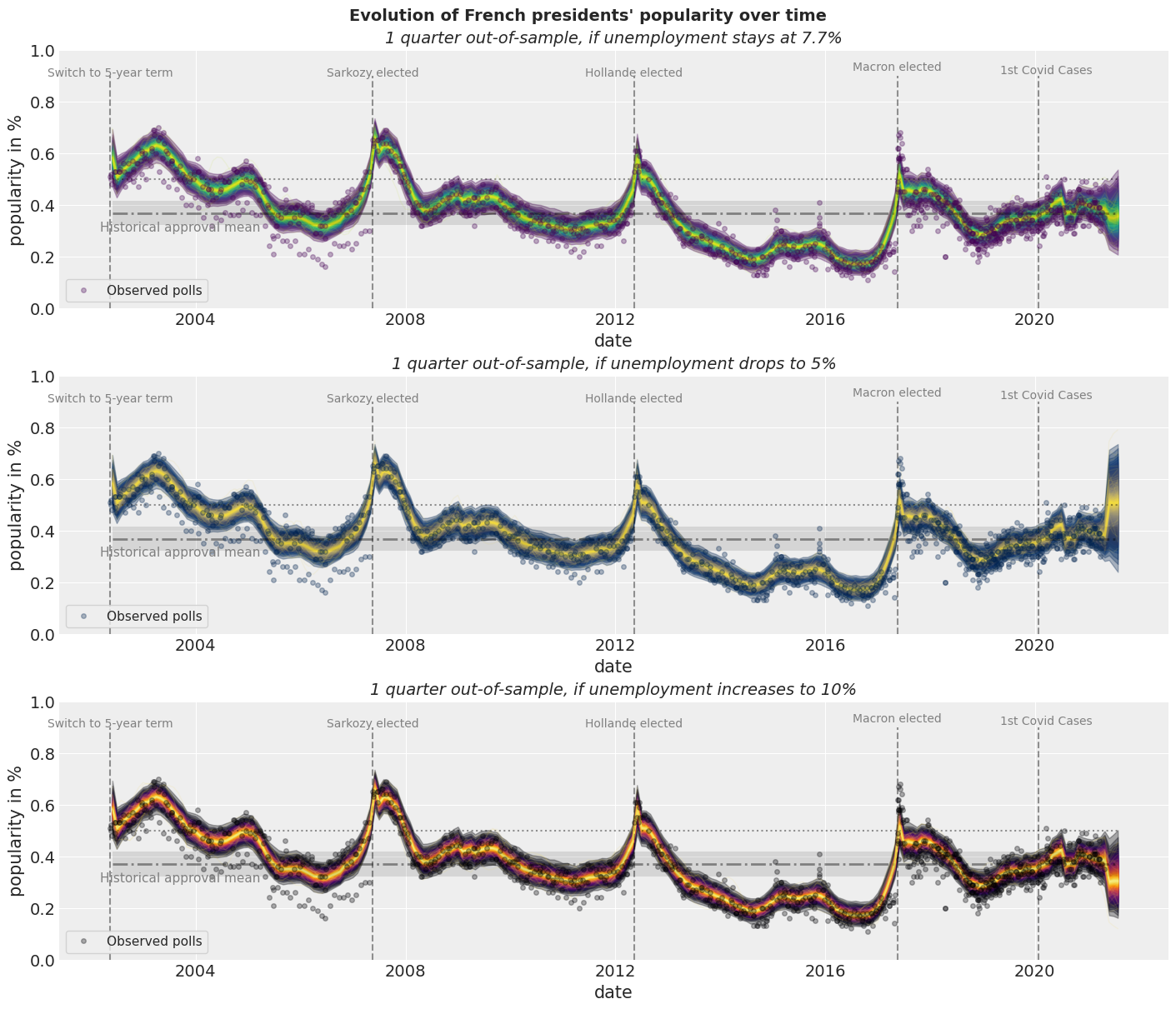
Some Applications

Time-Varying Regression Coefficients

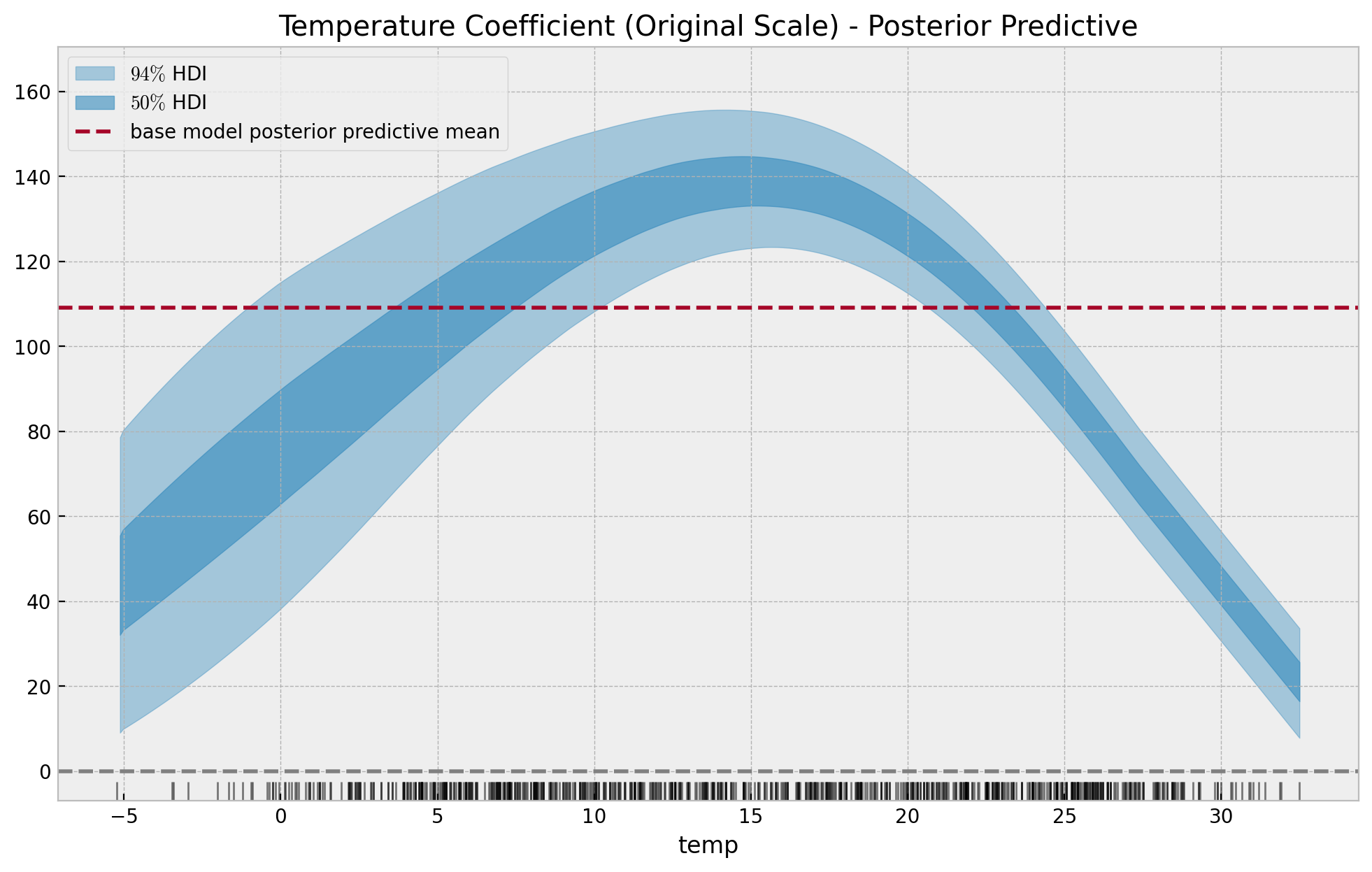
Time-Varying Regression Coefficients via Hilbert Space Gaussian Process Approximation

Some Applications

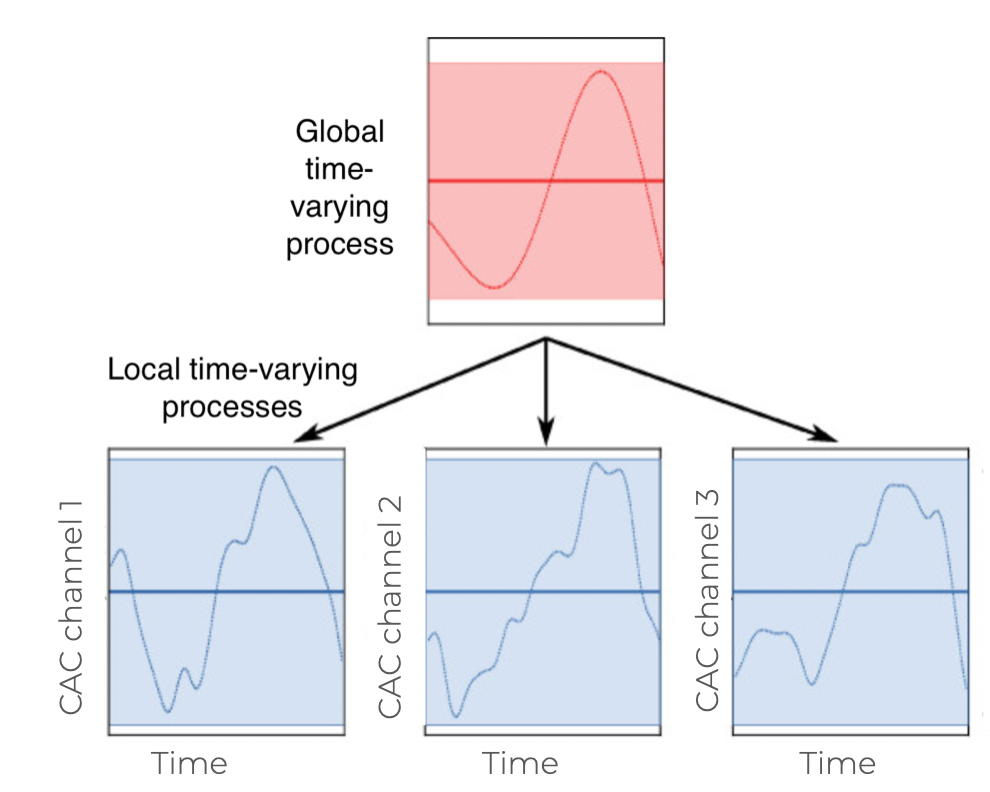
Changes in marketing effectiveness over time

Bayesian Media Mix Models: Modelling changes in marketing effectiveness over time

Gaussian Processes

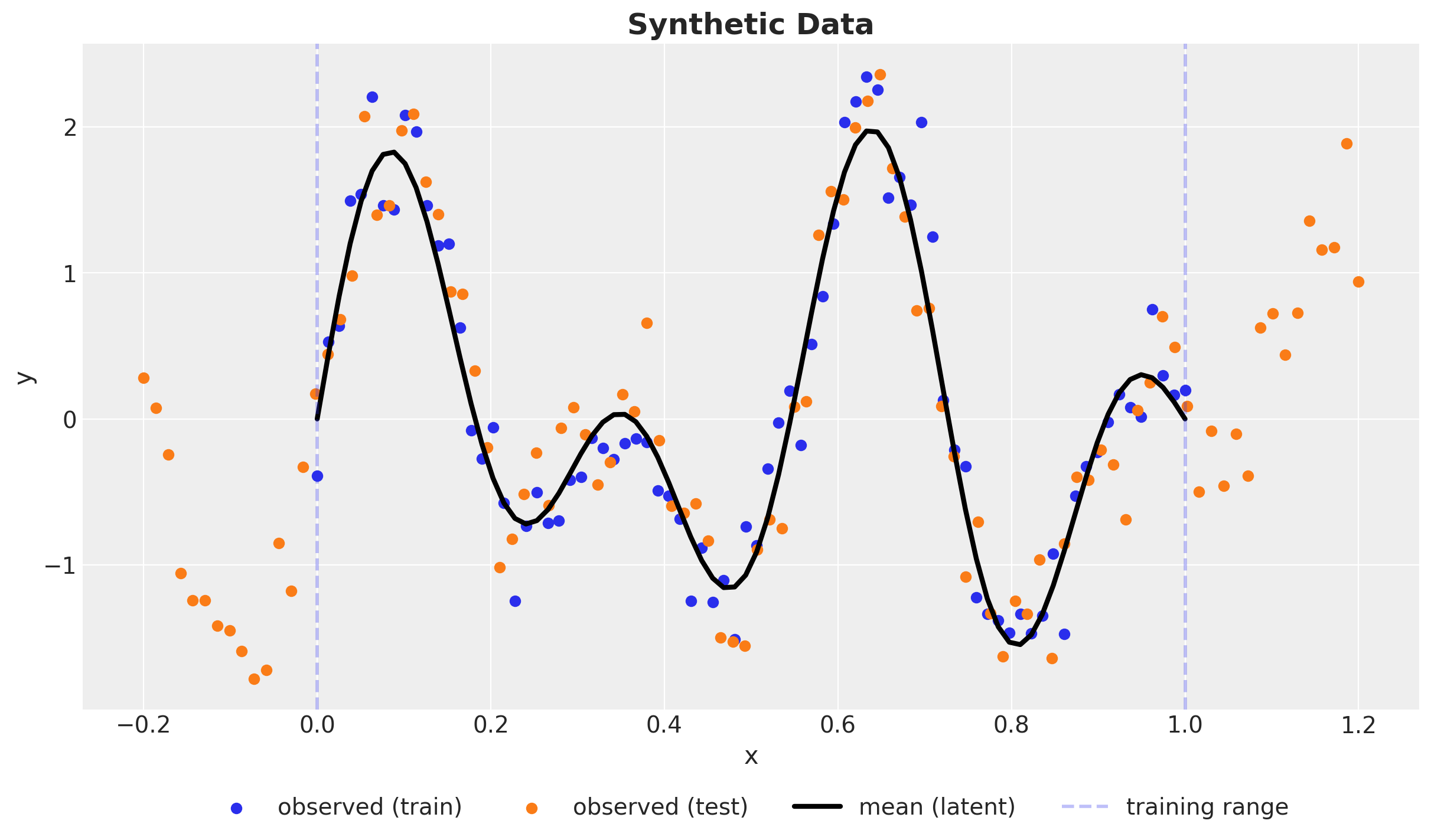
Synthetic Data

\(y \sim \text{Normal}(\sin(4 \pi x) + \sin(7 \pi x), 0.3^2)\)

Kernel

A way to encode similarity between points

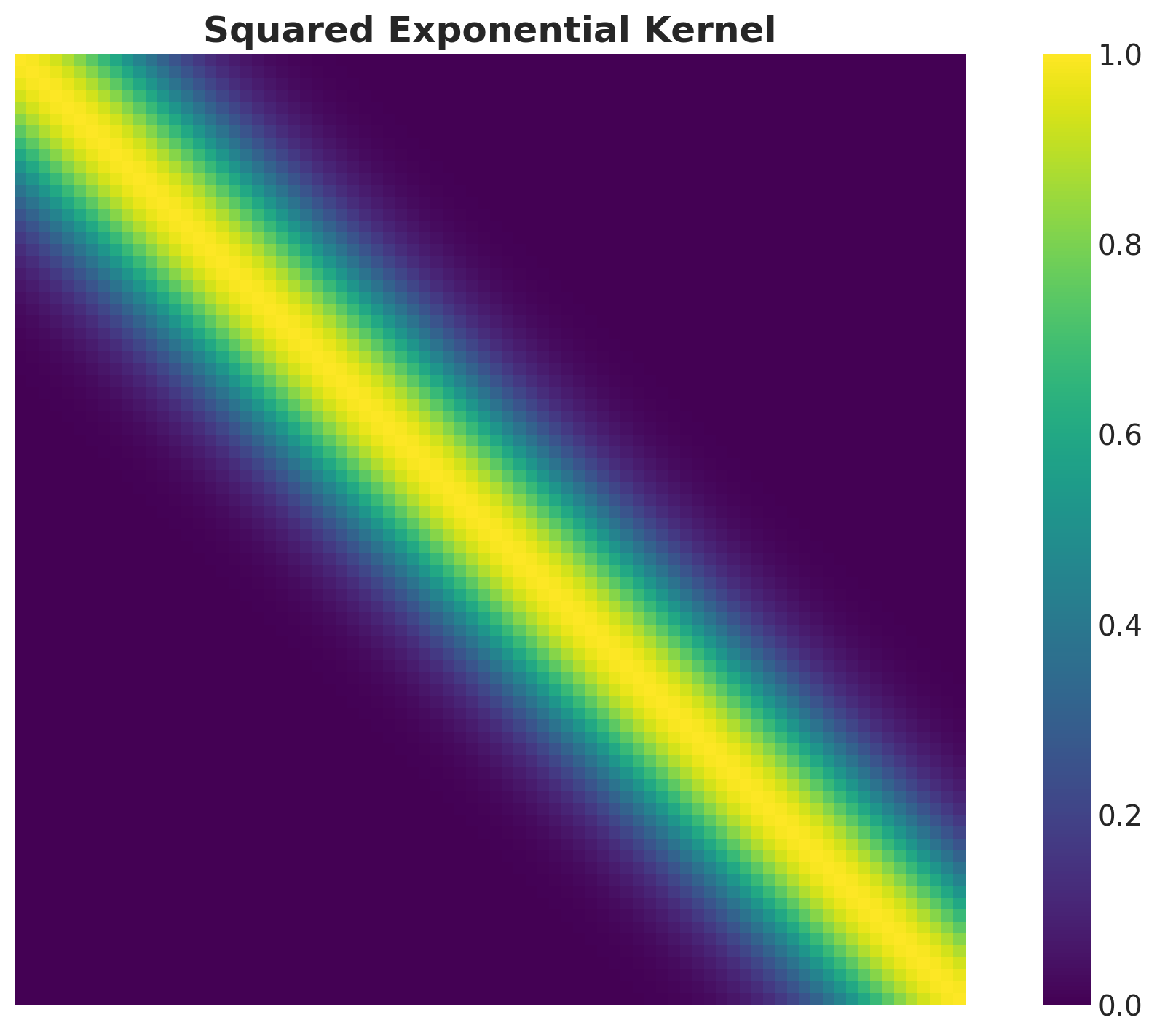
Example: Squared Exponential Kernel

\[ k(x, x') = a^ 2 \exp\left(-\frac{(x - x')^2}{2 \ell^2}\right) \]

Where \(a\) is the amplitude and \(\ell\) is the length-scale.

Note

Observe that the kernel just depends on the distance between points \(r = x - x'\). This is a property of stationary kernels.

Kernel Matrix

GP Model - Prior

Let us denote by \((x, y)\) and the training data and by \(x_{*}\) the test set for which we want to generate predictions. We define by \(f\) and \(f_*\) the latent functions for the training and test sets respectively.

\[ \left( \begin{array}{c} y \\ f_* \end{array} \right) \sim \text{MultivariateNormal}(0, \boldsymbol{K}) \]

where

\[ \boldsymbol{K} = \left( \begin{array}{cc} K(X, X) + \sigma^2_n I & K(X, X_*) \\ K(X_*, X) & K(X_*, X_*) \end{array} \right) \]

GP Model - Conditioning

\[ f_*|X, y, X_* \sim \text{MultivariateNormal}(\bar{f}_*, \text{cov}(f_*)) \]

where

\[ \begin{align*} \bar{f}_* &= K(X_*, X){\color{red}{(K(X, X) + \sigma^2_n I)^{-1}}} \\ \text{cov}(f_*) & = K(X_*, X_*) - K(X_*, X){\color{red}{(K(X, X) + \sigma^2_n I)^{-1}}} K(X, X_*) \end{align*} \]

Important

Taking the inverse of the kernel matrix is the most computationally expensive part of the GP model. It is of order \(\mathcal{O}(n^3)\).

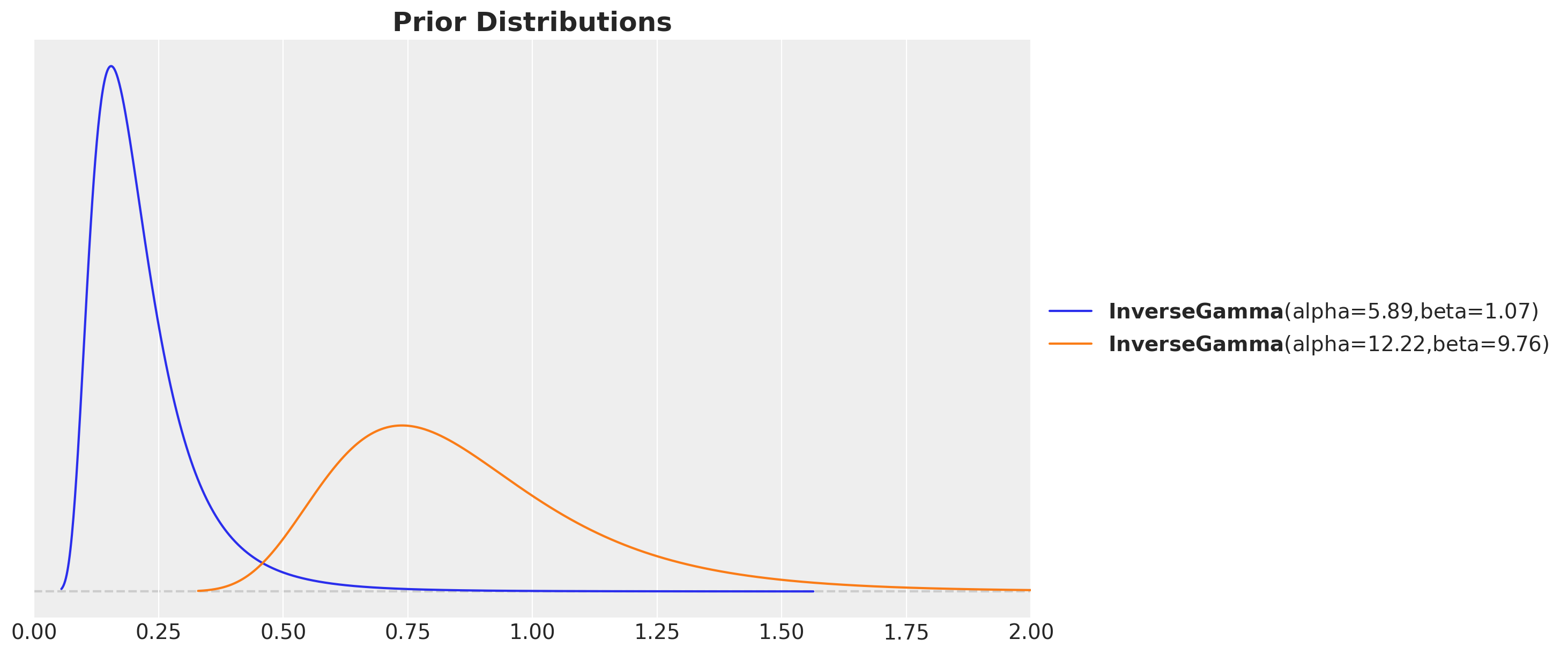
Kernel parameter priors

inverse_gamma_params_1 = pm.find_constrained_prior(
    distribution=pm.InverseGamma,
    lower=0.01,
    upper=0.4,
    init_guess={"alpha": 5, "beta": 3},
    mass=0.94,
)
inverse_gamma_params_2 = pm.find_constrained_prior(
    distribution=pm.InverseGamma,
    lower=0.5,
    upper=1.5,
    init_guess={"alpha": 5, "beta": 6},
    mass=0.94,
)

fig, ax = plt.subplots()
pz.InverseGamma(**inverse_gamma_params_1).plot_pdf(color="C0", ax=ax)
pz.InverseGamma(**inverse_gamma_params_2).plot_pdf(color="C1", ax=ax)
ax.set(xlim=(0, 2))
ax.set_title("Prior Distributions", fontsize=18, fontweight="bold");

Kernel parameter priors

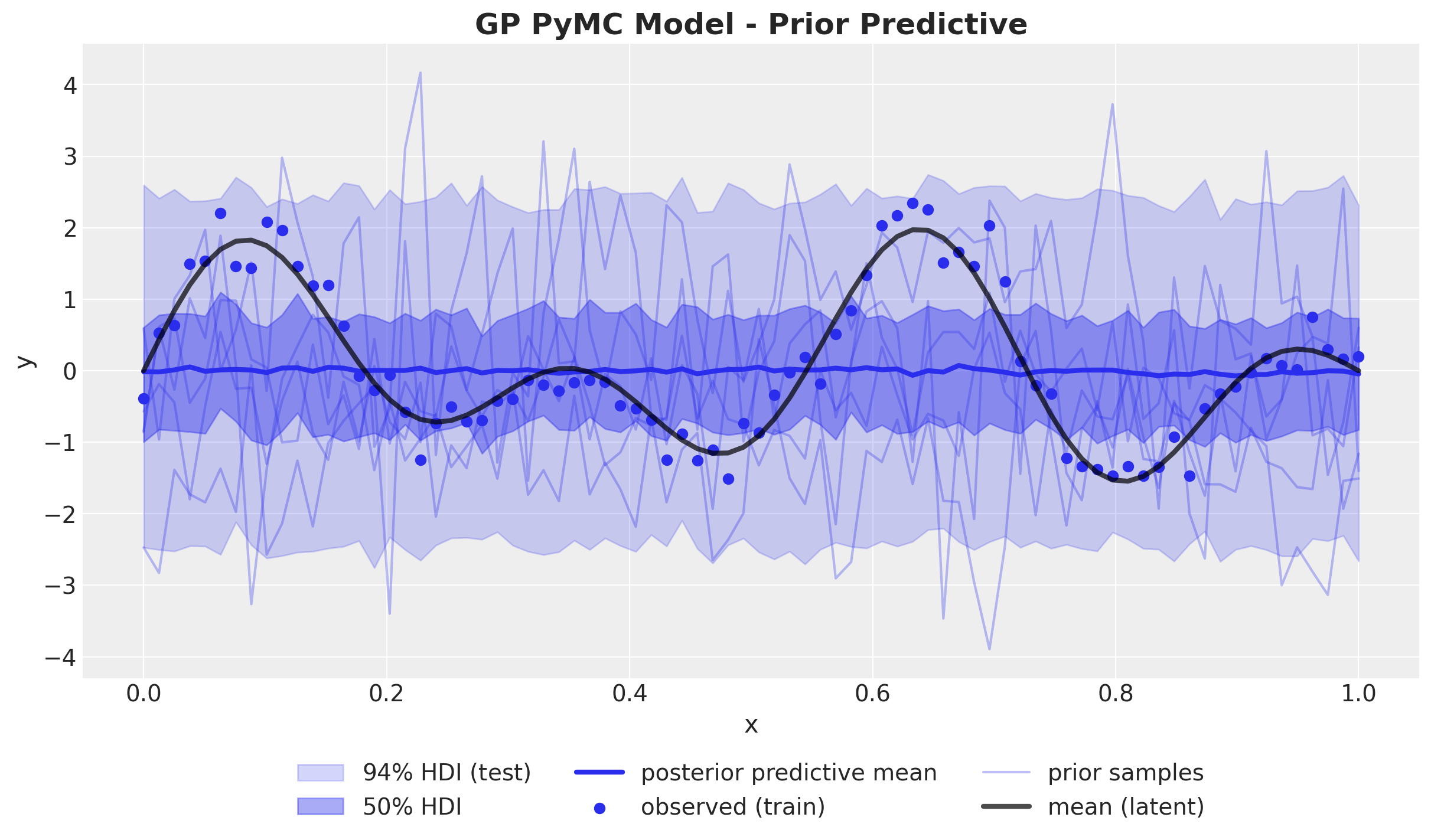
GP Model in PyMC

with pm.Model() as gp_pymc_model:
    x_data = pm.MutableData("x_data", value=x_train)

    kernel_amplitude = pm.InverseGamma("kernel_amplitude", ...)
    kernel_length_scale = pm.InverseGamma("kernel_length_scale", ...)
    noise = pm.InverseGamma("noise", ...)

    mean = pm.gp.mean.Zero()
    cov = kernel_amplitude**2 * pm.gp.cov.ExpQuad(
        input_dim=1, ls=kernel_length_scale
    )
    gp = pm.gp.Latent(mean_func=mean, cov_func=cov)
    f = gp.prior("f", X=x_data[:, None])

    pm.Normal("likelihood", mu=f, sigma=noise, observed=y_train_obs)

GP Model in PyMC

GP Model - Prior Predictions

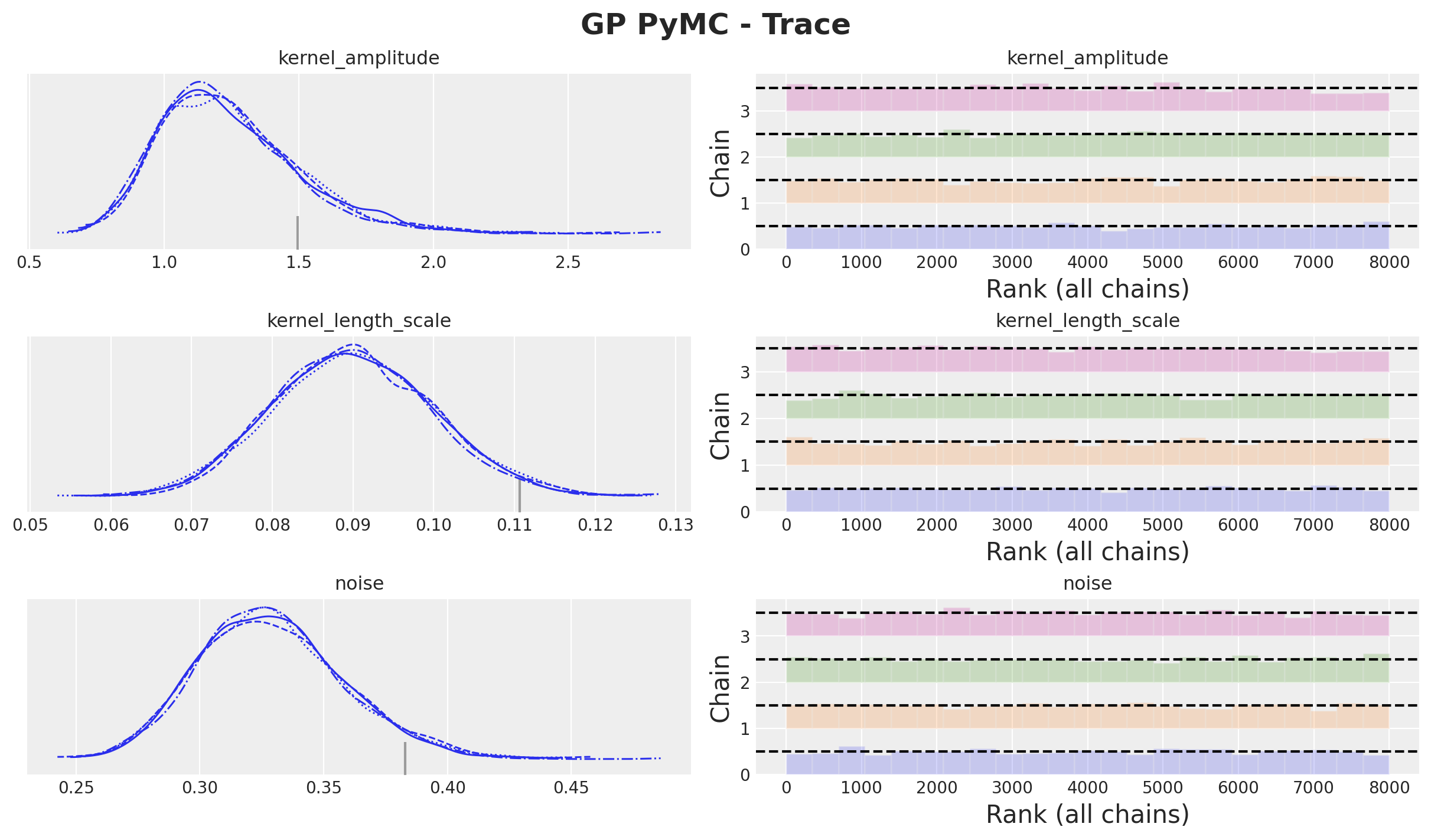
GP Model - Posterior Distributions

Out-of-Sample Predictions

conditional method

with gp_pymc_model:
    x_star_data = pm.MutableData("x_star_data", x_test)
    f_star = gp.conditional("f_star", x_star_data[:, None])
    pm.Normal("likelihood_test", mu=f_star, sigma=noise)

    gp_pymc_idata.extend(
        pm.sample_posterior_predictive(
            trace=gp_pymc_idata,
            var_names=["f_star", "likelihood_test"],
            random_seed=rng_subkey[1].item(),
        )
    )

GP Model - Posterior Predictive

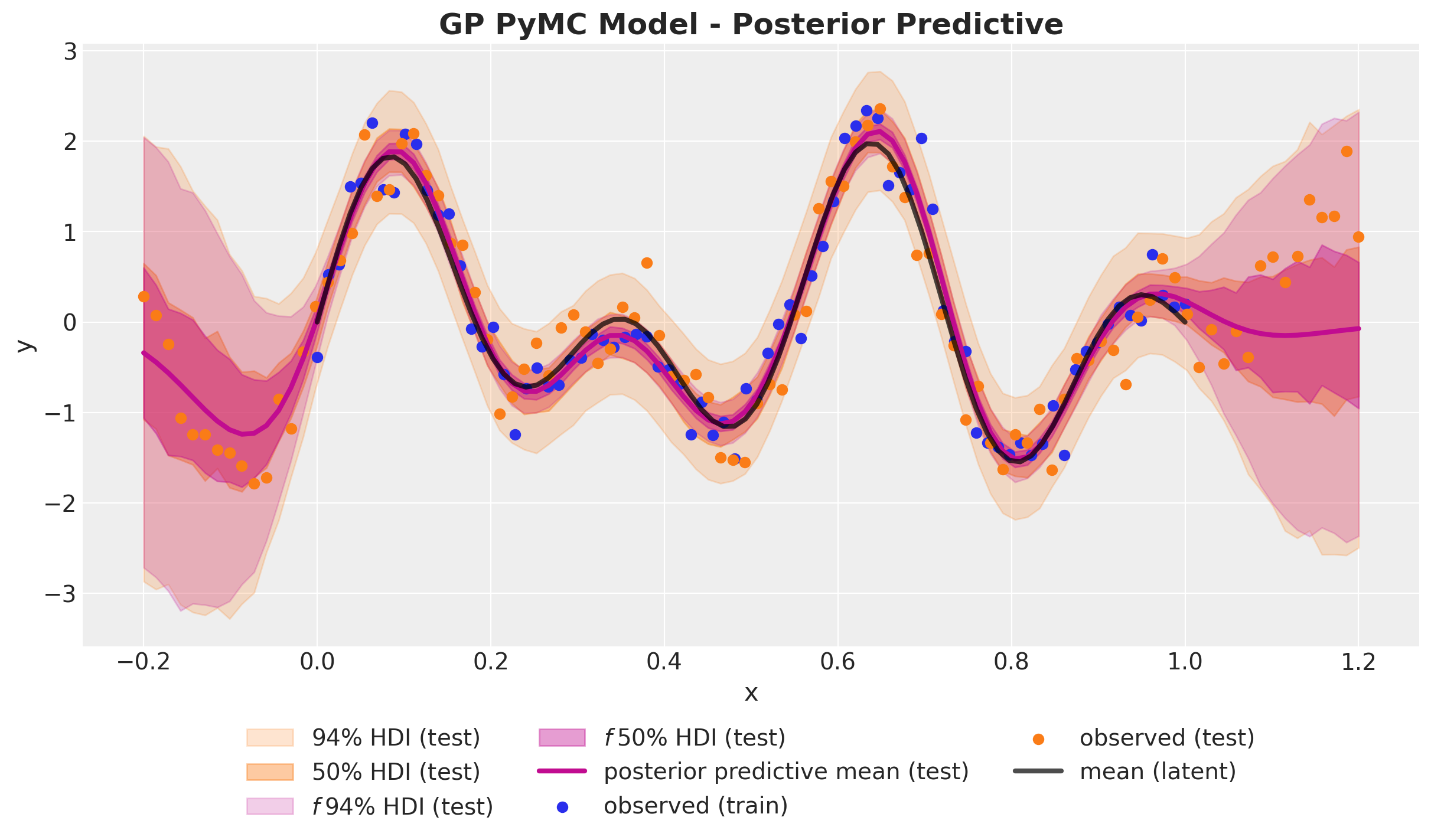
Hilbert Space Gaussian Process (HSGP) Approximation

HSGP Deep Dive

Approach Summary 🤓

  • Strategy: Approximate the Gram matrix \(K\) with a matrix \(\tilde{K}\) with a smaller rank \(m < n\).

  • Key Idea: Interpret the covariance function as the kernel of a pseudo-differential operator and approximate it using Hilbert space methods.

  • Result: A reduced-rank approximation for the covariance function, where the basis functions are independent of the covariance functions and their parameters (plus asymptotic convergence).

Hilbert space methods for reduced-rank Gaussian process regression

Hilbert Space Approximation

%%{init: {"theme": "white", "themeVariables": {"fontSize": "54px"}, "flowchart":{"htmlLabels": false}}}%%
flowchart TD
  kernel["kernel"] --> spectral_sensity["Spectral Density"]
  spectral_sensity --> polynomial["Polynomial Expansion"]
  laplacian["Laplacian"] --> fourier["Fourier Transform"]
  laplacian --> dirichlet["Dirichlet's BC"]
  dirichlet --> spectral_decomposition["Spectral Decomposition"]
  spectral_decomposition["Spectral Decomposition"] --> functional["Functional Calculus"]
  polynomial --> identify_coefficients["Identify Coefficients"]
  fourier --> identify_coefficients
  functional --> identify_coefficients
  identify_coefficients --> approximation["Approximation Formula"]

Hilbert Space Approximation

Approximation Strategy Steps

  1. D-Tour: Eigenvalues and Eigenvectors
  2. We recall the spectral density \(S(\omega)\) associated with a stationary kernel function \(k\).
  3. We approximate the spectral density \(S(\omega)\) as a polynomial series in \(||\omega||^2\).
  4. We can interpret these polynomial terms as powers of the Laplacian operator. The key observation is that the Fourier transform of the Laplacian operator is \(||\omega||^2\).
  5. Next, we impose Dirichlet boundary conditions on the Laplacian operator which makes it self-adjoint and with a discrete spectrum.
  6. We identify the expansion in (2) with the sum of powers of the Laplacian operator in the eigenbasis of (4).
  7. We arrive at the final approximation formula and explicitly compute the terms for the squared exponential kernel in the one-dimensional case.

Eigenvalues and Eigenvectors

Recall that given a matrix \(A\) (or a linear operator) the eigenvalues and eigenvectors are the solutions to the equation

\[A v = \lambda v\]

where \(v \neq \vec{0}\) is the eigenvector and \(\lambda\) is the eigenvalue.

The spectrum of a matrix is the set of its eigenvalues.

The Spectral Theorem for Matrices

Example - \(2 \times 2\) Matrix

\[ A = \begin{pmatrix} 1 & 2 \\ 2 & 1 \end{pmatrix} \]

The eigenvalues are \(\lambda_1 = 3\) and \(\lambda_2 = -1\) with eigenvectors:

\[ v_1 = \frac{1}{\sqrt{2}} \begin{pmatrix} 1 \\ 1 \end{pmatrix} \quad \text{and} \quad v_2 = \frac{1}{\sqrt{2}} \begin{pmatrix} -1 \\ 1 \end{pmatrix} \]

Properties

\[ v_1^{T} v_2 = 0 \quad \text{and} \quad v_1^{T} v_1 = v_2^{T} v_2 = 1 \]

The Spectral Theorem

The spectral theorem states that we can always find such orthonormal basis of eigenvectors for a symmetric matrix.

Observe that if we consider the change-of-basis matrix

\[ Q = \begin{pmatrix} v_1 & v_2 \end{pmatrix} \]

then we can write the matrix \(A\) in the new basis as

\[ D = Q^{T} A Q = \begin{pmatrix} 3 & 0 \\ 0 & -1 \end{pmatrix} \]

Code Example

import jax.numpy as jnp

A = jnp.array([[1.0, 2.0], [2.0, 1.0]])

# Compute eigenvalues and eigenvectors
eigenvalues, eigenvectors = jnp.linalg.eig(A)

print(f"Eigenvalues: {eigenvalues}\nEigenvectors:\n{eigenvectors}")

>> Eigenvalues: [ 3.+0.j -1.+0.j]
>> Eigenvectors:
>> [[ 0.70710678+0.j -0.70710678+0.j]
>> [ 0.70710678+0.j  0.70710678+0.j]]


# Change of basis matrix
Q = eigenvectors
Q.T @ A @ Q

>> Array([[ 3.00000000e+00+0.j,  4.44089210e-16+0.j],
       [ 6.10622664e-16+0.j, -1.00000000e+00+0.j]], dtype=complex128)

The Spectral Theorem for Matrices

Spectral Projections

Another important consequence of the spectral theorem is that we can decompose the matrix \(A\) as a sum of projections onto its eigenspaces. That is, we can write re-write \(A\) as

\[ A = \sum_{j=1}^{2} \lambda_i v_j v_j^{T} \]

Projections

Observe that the operator \(P_{j} = v_j v_j ^{T}\) is indeed a projection operator, that is \(P^2 = P\) and \(P^T = P\), since the \(v_j\) constitutes an orthonormal basis.

Code Example

def proj(v, x):
    return jnp.dot(v, x) * v

def matrix_proj(x):
    return eigenvalues[0] * proj(Q[:, 0], x) + eigenvalues[1] * proj(Q[:, 1], x)

# First eigenvector
matrix_proj(Q[:, 0])  / eigenvalues[0]
>> Array([0.70710678+0.j, 0.70710678+0.j], dtype=complex128)

# Second eigenvector
matrix_proj(Q[:, 1])  / eigenvalues[1]
>> Array([-0.70710678-0.j,  0.70710678-0.j], dtype=complex128)

# Arbitrary vector
v = jnp.array([1.0, 2.0])
jnp.allclose(jnp.dot(A, v), matrix_proj(v))
>> Array(True, dtype=bool)

Functional Calculus

The functional calculus is a generalization of the Taylor series for functions to operators. Given a function \(f\) we can define the operator \(f(A)\) as

\[ f(A) = \sum_{j=1}^{2} \color{red}{f(\lambda_j)} \color{blue}{v_j v_j^{T}} \]

Examples

  • \(f(z) = z\) we recover the operator \(A\).
  • \(f(z) = 1\) we get the identity operator \(I\).
  • \(f(z) = z^2\) we get the operator \(A^2\).
  • \(f(z) =e^{z}\) we get the operator \(\exp(A)\).

Example: Exponential of a Matrix

Consider the exponential of the matrix \(A\) defined as

\[ \exp(A) = \sum_{j=0}^{\infty} \frac{A^j}{j!} \]

scipy.linalg.expm(A)
>> Array([[10.22670818,  9.85882874],
       [ 9.85882874, 10.22670818]], dtype=float64)

Example: Exponential of a Matrix

On the other hand, we can use the fact that \(A = Q D Q^{T}\) and that \(Q\) is an orthogonal matrix to write

\[ \exp(A) = \sum_{j=0}^{\infty} \frac{(Q D Q^{T})^j}{j!} = Q \left(\sum_{j=0}^{\infty} \frac{D^j}{j!}\right) Q^{T} = Q \exp(D) Q^{T} \]

and observe that \(\exp(D)\) is a diagonal matrix with the exponential of the diagonal elements:

Q @ jnp.diag(jnp.exp(eigenvalues)) @ Q.T
>> Array([[10.22670818+0.j,  9.85882874+0.j],
       [ 9.85882874+0.j, 10.22670818+0.j]], dtype=complex128)

Spectral Densities

In the case a kernel function is stationary, we can use the spectral representation of the kernel function (Bochner’s theorem):

\[ k(r) = \frac{1}{(2 \pi)^{d}}\int_{\mathbb{R}^{d}} e^{i \omega^{T} r} d\mu(\omega) \]

where \(\mu\) is a positive measure. If this measure has a density, it is called the spectral density \(S(\omega)\) corresponding to the covariance function, i.e. \(d\mu(\omega) = S(\omega) d\omega\).

Gaussian Processes for Machine Learning - Chapter 4: Covariance Functions.

Spectral Density - Example

For the squared exponential kernel, it can be shown that

\[ S(\omega) = a^2(2 \pi \ell^2)^{d/2} \exp\left(-2\pi^2\ell^2\omega^2\right) \]

For the special case \(d=1\) we have

\[ S(\omega) = a^2 \sqrt{2 \pi} \ell \exp\left(-2\pi^2\ell^2\omega^2\right) \]

Tip

Note the similarity between the spectral density and the Fourier transform. For Gaussian-like kernels, like the squared exponential, we expect the associated spectral density to also be Gaussian-like.

\(S(\omega)\) Squared Exponential

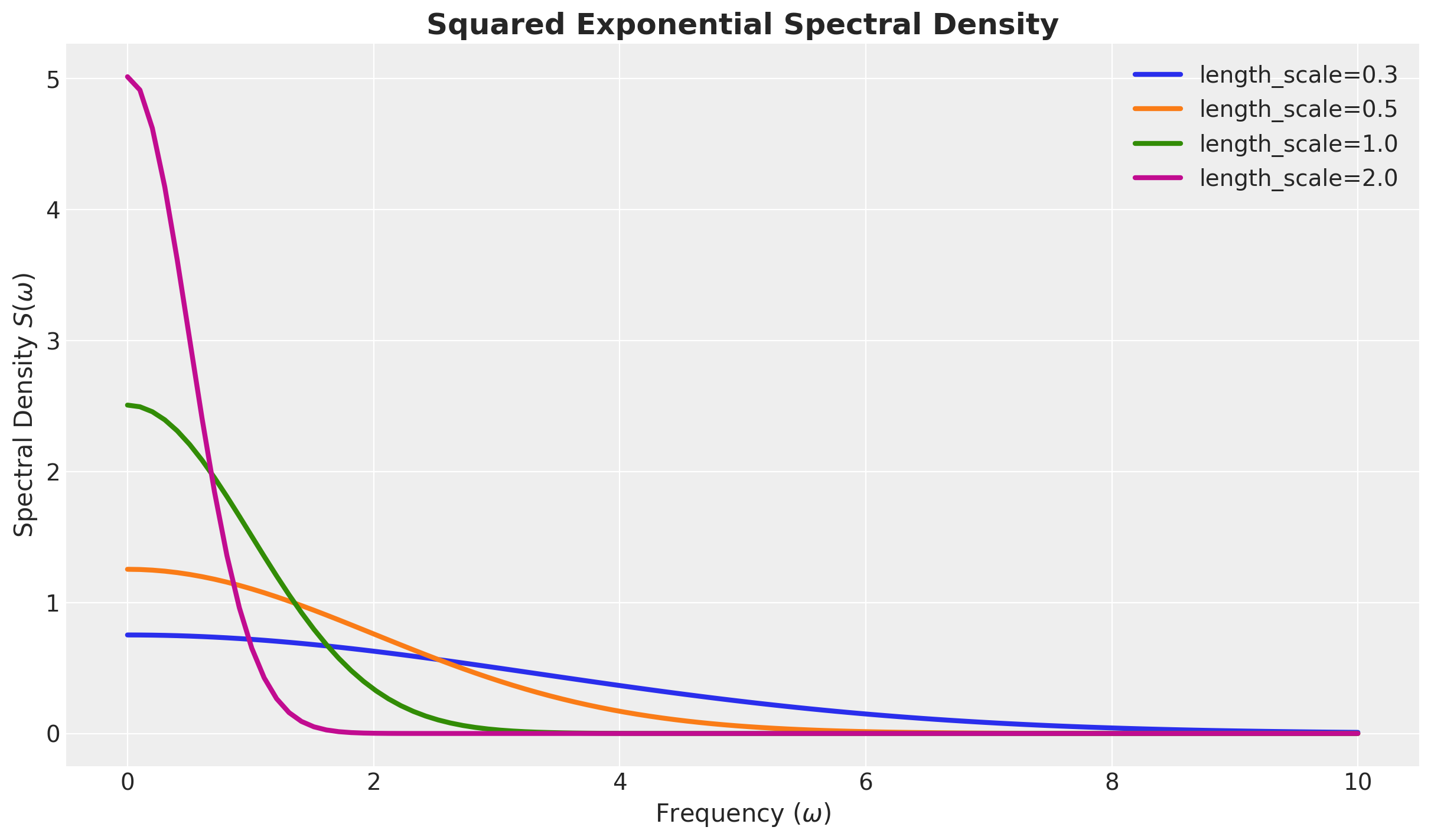
Formal Power Expansion of the Spectral Density

Let us assume the kernel function is isotropic, i.e. it just depends on the Euclidean norm \(||r||\).

  • \(S(\omega)\) is also isotropic.

  • Write \(S(||\omega||) = \psi(||\omega||^2)\) for a suitable function \(\psi\).

  • We can expand \(\psi\) (Taylor-like expansion)

    \[ \begin{align*} \psi(||\omega||^2) = a_0 + a_1 (||\omega||^2) + a_2 (||\omega||^2)^2 + a_3 (||\omega||^2)^3 + \cdots \end{align*} \]

The Laplace Operator

Recall the Laplace operator is defined as

\[ - \nabla^2 f = \sum_{i=1}^{d} \frac{\partial^2 f}{\partial x_i^2} \]

Tip

The Laplacian has many good properties:

  • Positive semi-definite

  • Elliptic

  • Self-adjoint (appropriate boundary conditions)

Unbounded Self-adjoint Operators on Hilbert Space

Kernel as a function of \(\nabla^2\)

One can verify that the Fourier transform of the Laplacian is

\[ \mathcal{F}[\nabla^2 f](\omega) = - ||\omega||^2 \mathcal{F}[f] \]

We can write the integral operator associated with the kernel

\[ \mathcal{K} := \int_{\mathbb{R}^d} k(\cdot, x')\phi(x') dx' \]

as

\[ \mathcal{K} = a_0 + a_1 (- \nabla^2) + a_2 (-\nabla^2)^2 - a_3 (-\nabla^2)^3 + \cdots \]

Dirichlet’s Laplacian

Boundary Conditions?

The most common boundary conditions are the Dirichlet boundary conditions, which are defined by requiring that the function vanishes on the boundary of the domain.

\[ \begin{align*} -\nabla^2 f &= \lambda f \quad \text{in} \quad \Omega \\ f &= 0 \quad \text{on} \quad \partial \Omega \end{align*} \]

Unbounded Self-adjoint Operators on Hilbert Space

Dirichlet’s Laplacian - Spectrum

  • It is is a self-adjoint operator defined on the Hilbert space \(L^{2}(\Omega)\) equipped with the Lebesgue measure. That is,

    \[ \int_{\Omega} (-\nabla^2 f(x)) g(x) dx = \int_{\Omega} f(x) (-\nabla^2 g(x)) dx \]

  • It has discrete spectrum with eigenvalues \(\lambda_j \rightarrow \infty\) and eigenfunctions \(\phi_j\) that form an orthonormal basis of \(L^2(\Omega)\), so that \[ \int_{\Omega} \phi_{j}(x) \phi_{k}(x) dx = \delta_{jk} \]

Example - One Dimensional Box

\(\Omega = [-L, L] \subset \mathbb{R}\)

\[ \frac{d^2 \phi}{dx^2} = - \lambda \phi \quad \text{with} \quad \phi(-L) = \phi(L) = 0 \]

Spectrum?

\[ \phi_j(x) = \sqrt{\frac{1}{L}} \sin\left(\frac{\pi j (x + L)}{2L}\right) \quad \text{and} \quad \lambda_j = \left(\frac{j \pi}{2L}\right)^2 \]

for \(j = 1, 2, \ldots\).

HSGP: Functional Calculus

\[ -\nabla^2 f(x) = \int_{\Omega} \overbrace{\left[\sum_{j} \lambda_{j} \phi_{j}(x) \phi_{j}(x')\right]}^{l(x, x')} f(x') dx' \]

We can construct powers of \(-\nabla^2\) as

\[ (- \nabla^2)^{s} f(x) = \int_{\Omega} {\color{red}{\overbrace{\left[\sum_{j} \lambda_{j}^{s} \phi_{j}(x) \phi_{j}(x')\right]}^{l^s(x, x')}}} f(x') dx'. \]

HSGP: Coefficients Identification

Use the formal expansion of \(\mathcal{K}\) in terms of powers of \(\nabla^2\):

\[ \begin{align*} & \left[ a_{0} + a_{1}(-\nabla^2) + a_{2}(-\nabla^2)^2 + \cdots \right]f(x) = \\ &\int_{\Omega} \left[a_{0} + a_{1} l(x, x') + a_{2} l^{2}(x, x') + \cdots \right] f(x') dx' \end{align*} \]

This implies we can approximate the kernel as

\[ \begin{align*} k(x, x') \approx & \: a_{0} + a_{1} l(x, x') + a_{2} l^{2}(x, x') + \cdots \\ \approx & \sum_{j} {\color{red}{\underbrace{\left[ a_{0} + a_{1} \lambda_{j} + a_{2} \lambda_{j}^2 + \cdots \right]}_{S(\sqrt{\lambda_{j}})}}} \phi_{j}(x) \phi_{j}(x') \end{align*} \]

HSGP: Final Formula

In summary, we have the following approximation formula for the kernel function:

\[ \boxed{ k(x, x') \approx \sum_{j}^{m} \color{red}{S(\sqrt{\lambda_j})}\color{blue}{\phi_{j}(x) \phi_{j}(x')} } \]

That is, the model of the Gaussian process \(f\) can be written as

\[ f(x) \sim \text{MultivariateNormal}(\boldsymbol{\mu}, \Phi\mathcal{D}\Phi^{T}) \]

where \(\mathcal{D} = \text{diag}(S(\sqrt{\lambda_1}), S(\sqrt{\lambda_2}), \ldots, S(\sqrt{\lambda_{m}}))\).

HSGP: Linear Model

\[ f(x) \approx \sum_{j = 1}^{m} \overbrace{\color{red}{\left(S(\sqrt{\lambda_j})\right)^{1/2}}}^{\text{all hyperparameters are here!}} \times \underbrace{\color{blue}{\phi_{j}(x)}}_{\text{easy to compute!}} \times \overbrace{\color{green}{\beta_{j}}}^{\sim \: \text{Normal}(0,1)} \]

Note

The only dependence on the hyperparameters is through the spectral density.

Computational Cost

The computational cost of evaluating the log posterior density of univariate HSGPs scales as \(\mathcal{O}(nm + m)\).

Squared Exponential \(1\)-dim

\[ \begin{align*} k(x, x') \approx \sum_{j=1}^{m} & \color{red}{\overbrace{\left(a^2 \sqrt{2 \pi} \ell \exp\left(-2\pi^2\ell^2 \left(\frac{\pi j}{2L}\right)^2 \right)\right)^{1/2}}^{\left(S(\sqrt{\lambda_j})\right)^{1/2}}} \\ & \times \color{blue}{\overbrace{\left(\sqrt{\frac{1}{L}} \sin\left(\frac{\pi j (x + L)}{2L}\right)\right)}^{\phi_{j}(x)}} \\ & \times \color{green}{\overbrace{\beta_{j}}^{\sim \: \text{Normal}(0, 1)}} \end{align*} \]

Hilbert Space Approximation (Recap)

%%{init: {"theme": "white", "themeVariables": {"fontSize": "54px"}, "flowchart":{"htmlLabels":false}}}%%
flowchart TD
  kernel["kernel"] --> spectral_sensity["Spectral Density"]
  spectral_sensity --> polynomial["Polynomial Expansion"]
  laplacian["Laplacian"] --> fourier["Fourier Transform"]
  laplacian --> dirichlet["Dirichlet's BC"]
  dirichlet --> spectral_decomposition["Spectral Decomposition"]
  spectral_decomposition["Spectral Decomposition"] --> functional["Functional Calculus"]
  polynomial --> identify_coefficients["Identify Coefficients"]
  fourier --> identify_coefficients
  functional --> identify_coefficients
  identify_coefficients --> approximation["Approximation Formula"]

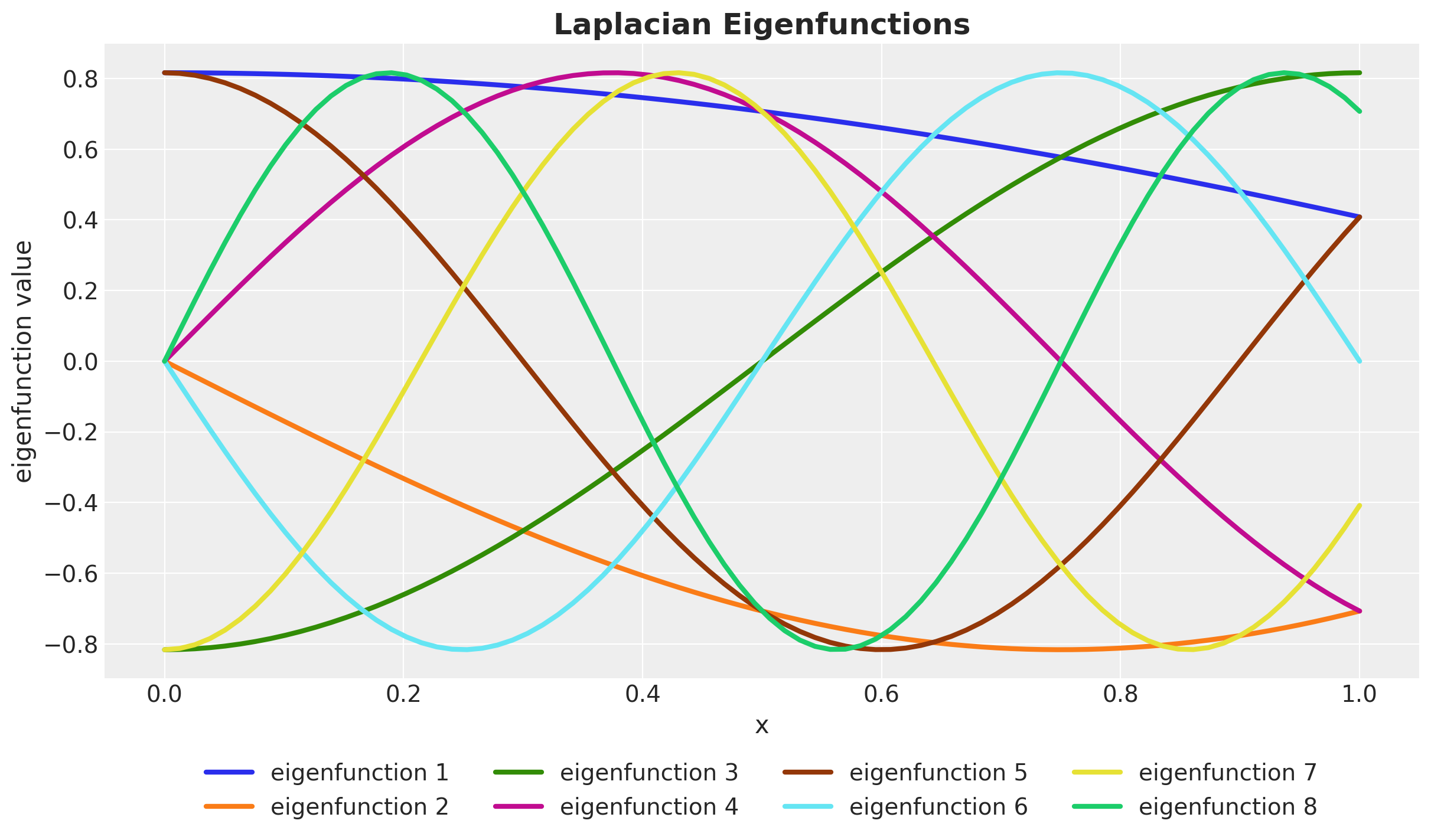
Laplace Eigenfunctions

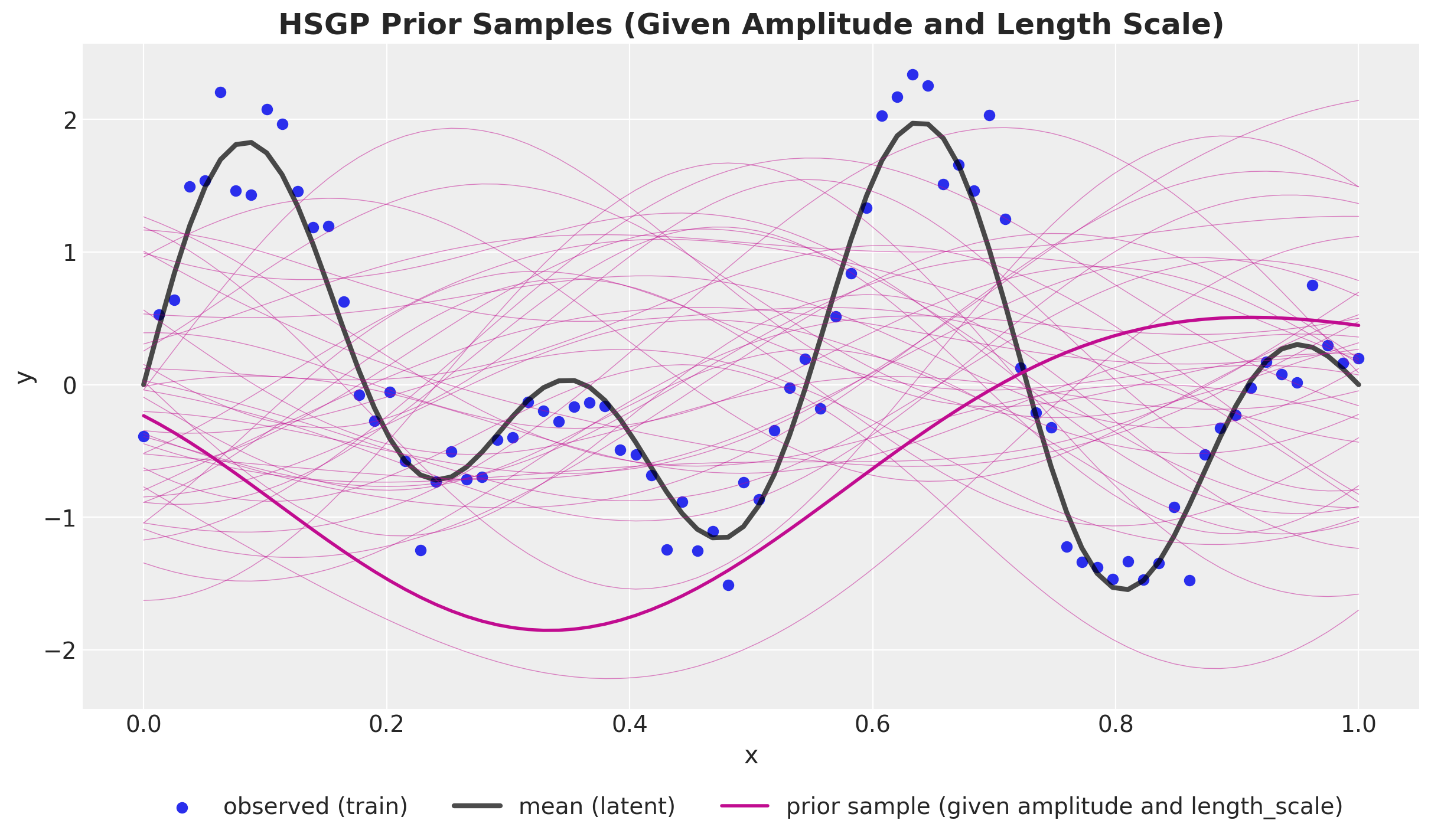
Back to the example …

Prior Predictive

PyMC Implementation

HSGP Class

with pm.Model() as hsgp_pymc_model:
    x_data = pm.MutableData("x_data", value=x_train)
    y_data = pm.MutableData("y_data", y_train_obs)

    kernel_amplitude = pm.InverseGamma("kernel_amplitude", ...)
    kernel_length_scale = pm.InverseGamma("kernel_length_scale", ...)
    noise = pm.InverseGamma("noise", ...)

    mean = pm.gp.mean.Zero()
    cov = kernel_amplitude**2 * pm.gp.cov.ExpQuad(
        input_dim=1, ls=kernel_length_scale
    )
    gp = pm.gp.HSGP(m=[20], L=[1.3], mean_func=mean, cov_func=cov)
    f = gp.prior("f", X=x_data[:, None])

    pm.Normal("likelihood", mu=f, sigma=noise, observed=y_data)

Out-of-Sample Predictions

conditional method

with hsgp_pymc_model:
    x_star_data = pm.MutableData("x_star_data", x_test)
    f_star = gp.conditional("f_star", x_star_data[:, None])
    pm.set_data({"x_data": x_test, "y_data": np.ones_like(x_test)})
    hsgp_pymc_idata.extend(
        pm.sample_posterior_predictive(
            trace=hsgp_pymc_idata,
            var_names=["f_star", "likelihood"],
            random_seed=rng_subkey[1].item(),
        )
    )

HSGP Model - Posterior Predictive

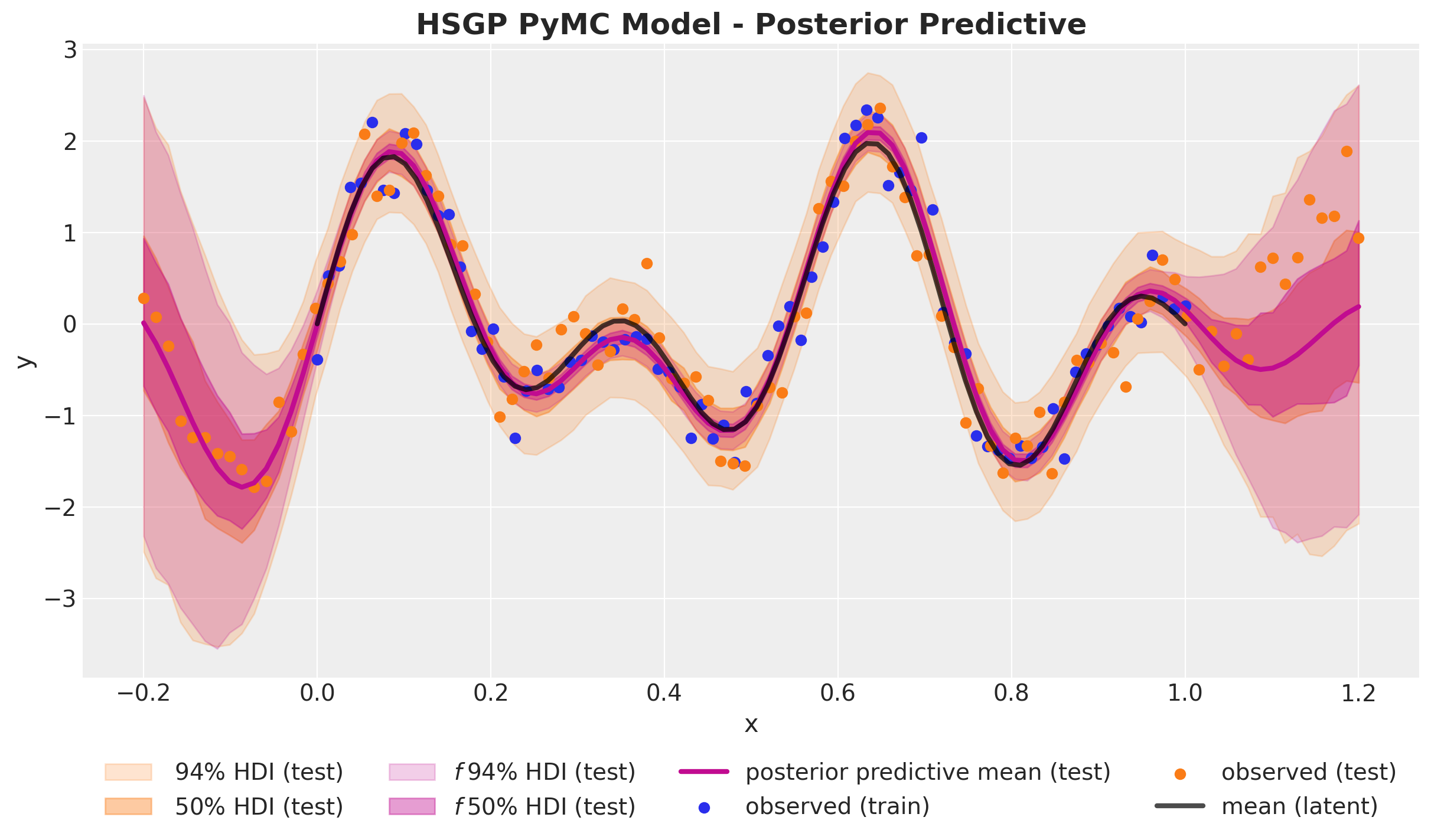
PyMC Implementation

HSGP.prior_linearized

with pm.Model() as hsgp_linearized_pymc_model:
    x_data = pm.MutableData("x_data", value=x_train)
    y_data = pm.MutableData("y_data", y_train_obs)

    kernel_amplitude = pm.InverseGamma("kernel_amplitude", ...)
    kernel_length_scale = pm.InverseGamma("kernel_length_scale", ...)
    noise = pm.InverseGamma("noise", ...)

    mean = pm.gp.mean.Zero()
    cov = kernel_amplitude**2 * pm.gp.cov.ExpQuad(input_dim=1, ls=kernel_length_scale)
    gp = pm.gp.HSGP(m=[20], L=[1.3], mean_func=mean, cov_func=cov)
    phi, sqrt_psd = gp.prior_linearized(Xs=x_data_centered[:, None])

    beta = pm.Normal("beta", mu=0, sigma=1, size=gp._m_star)
    f = pm.Deterministic("f", phi @ (beta * sqrt_psd))

    pm.Normal("likelihood", mu=f, sigma=noise, observed=y_data)

Out-of-Sample Predictions

pm.set_data method

with hsgp_pymc_model:
    pm.set_data({"x_data": x_test, "y_data": np.ones_like(x_test)})
    hsgp_linearized_pymc_idata.extend(
        pm.sample_posterior_predictive(
            trace=hsgp_pymc_idata,
            var_names=[
                "f",
                "likelihood",
            ],
            random_seed=rng_subkey[1].item(),
        )
    )

Example: Birthdays Dataset

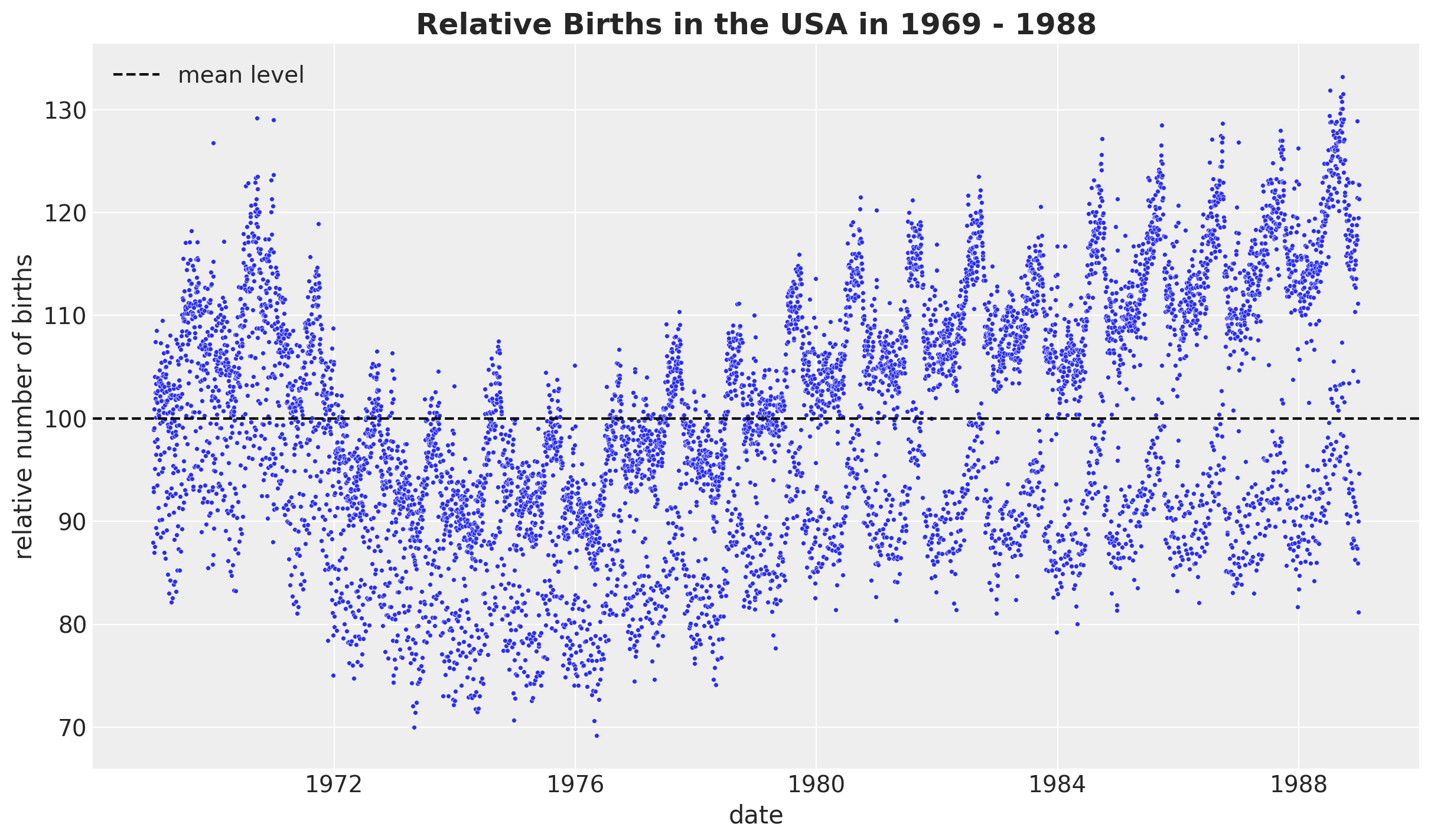
The Birthdays Dataset

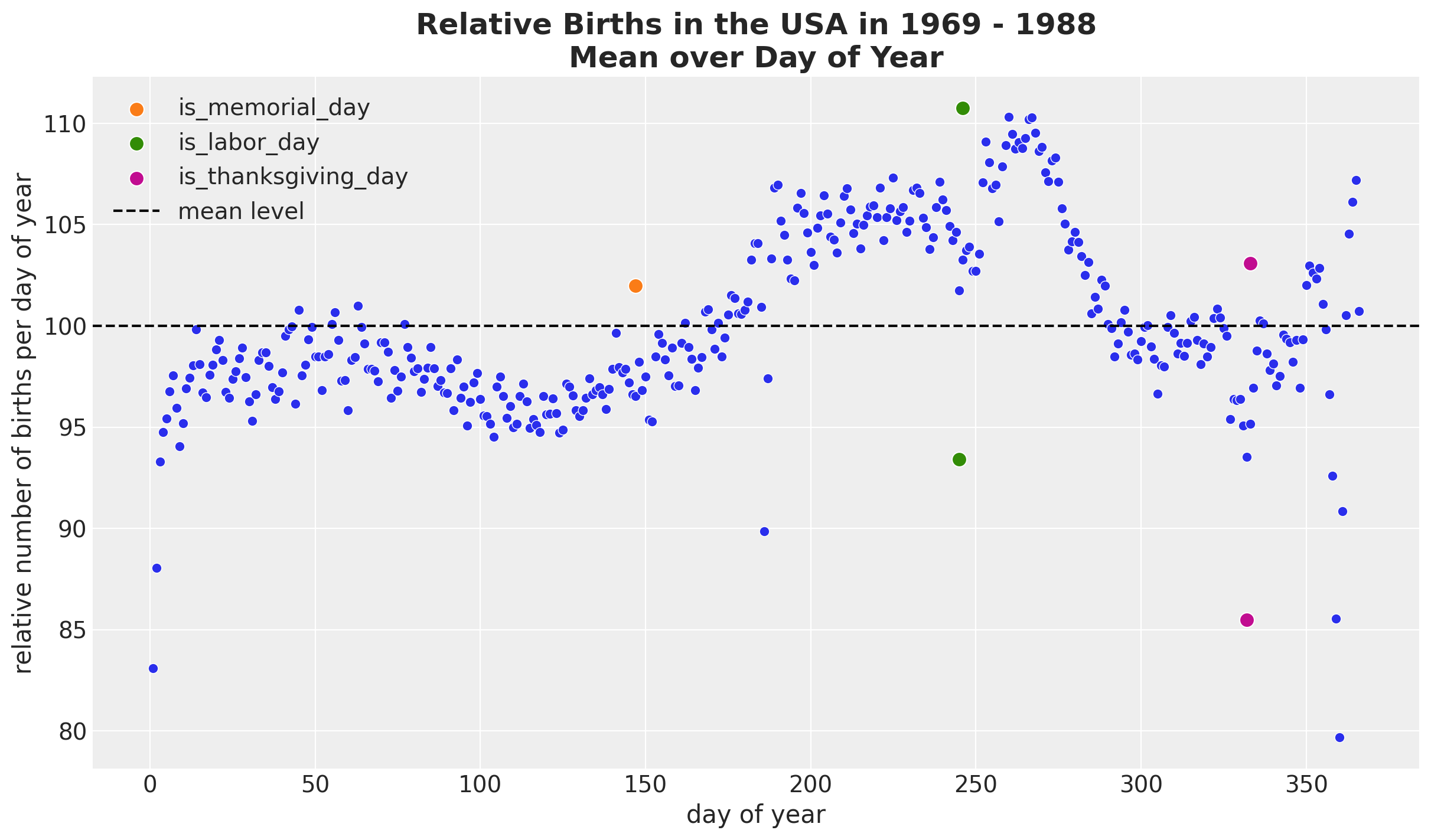
Time Series Modeling with HSGP: Baby Births Example

Seasonal Patterns - Day of Year

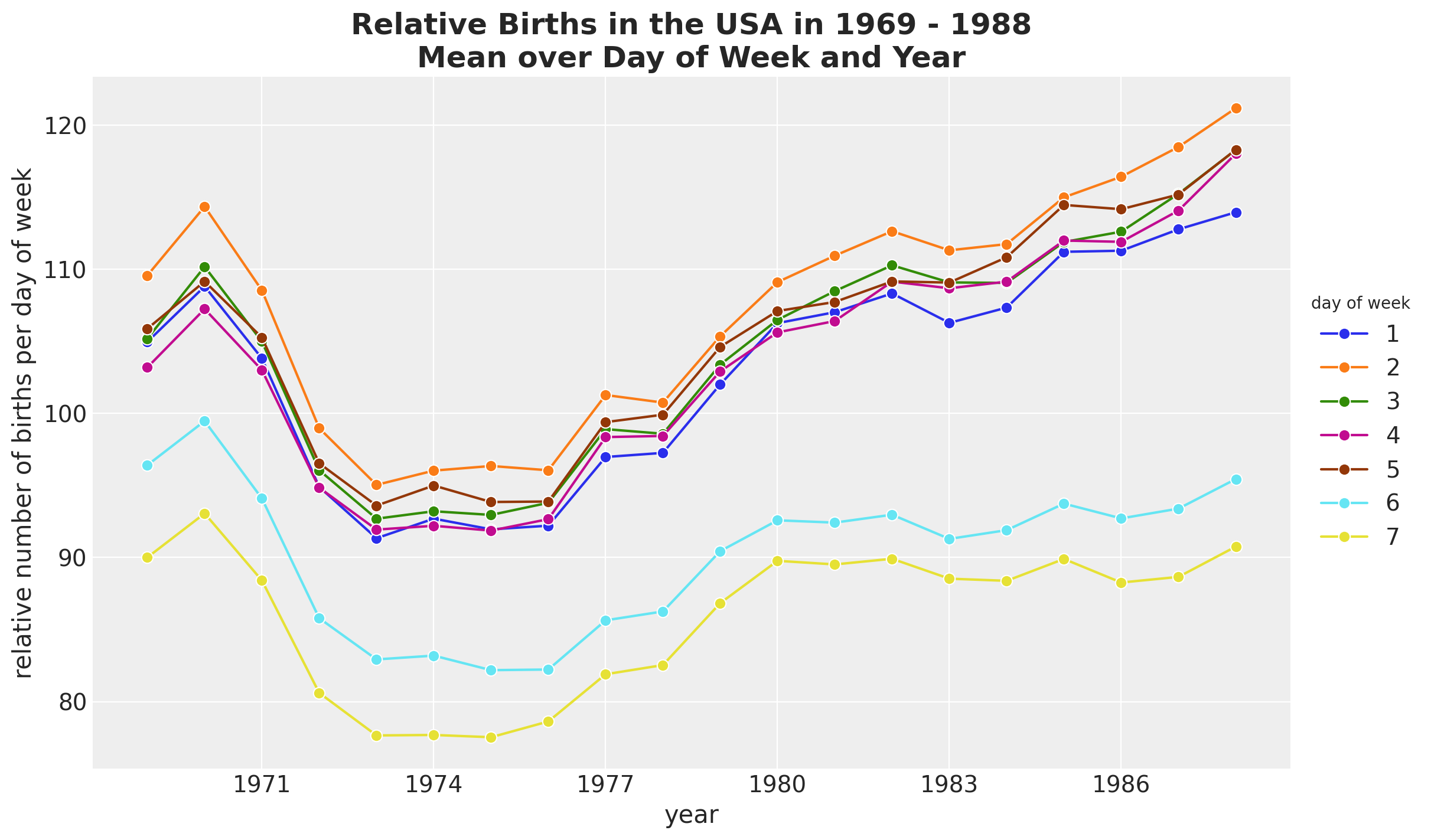
Seasonal Patterns - Day of Week

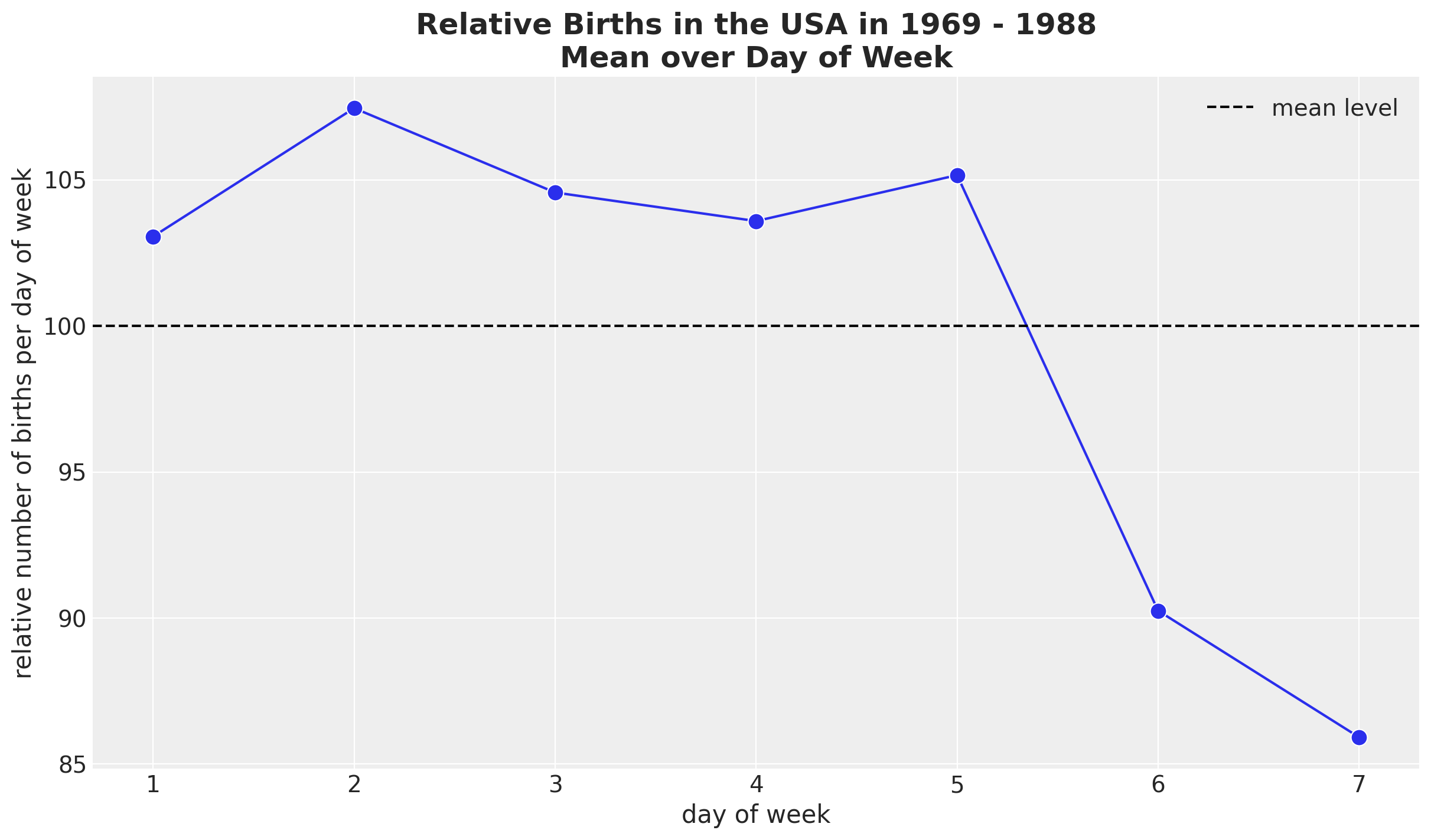
Seasonal Patterns - Day of Week

HSGP Model - Trend

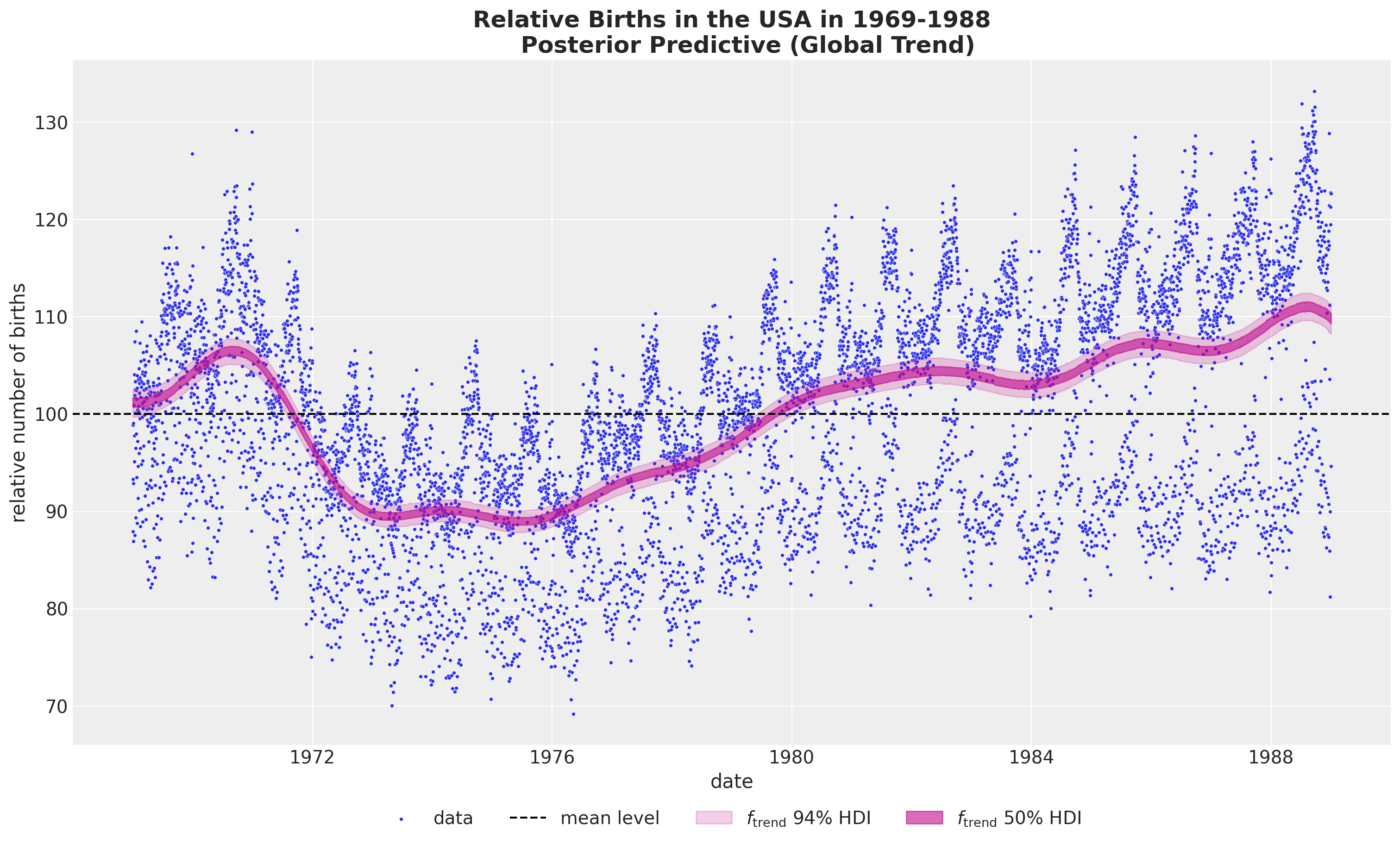
We use a Gaussian process with a squared exponential kernel.

HSGP Model - Yearly Seasonality

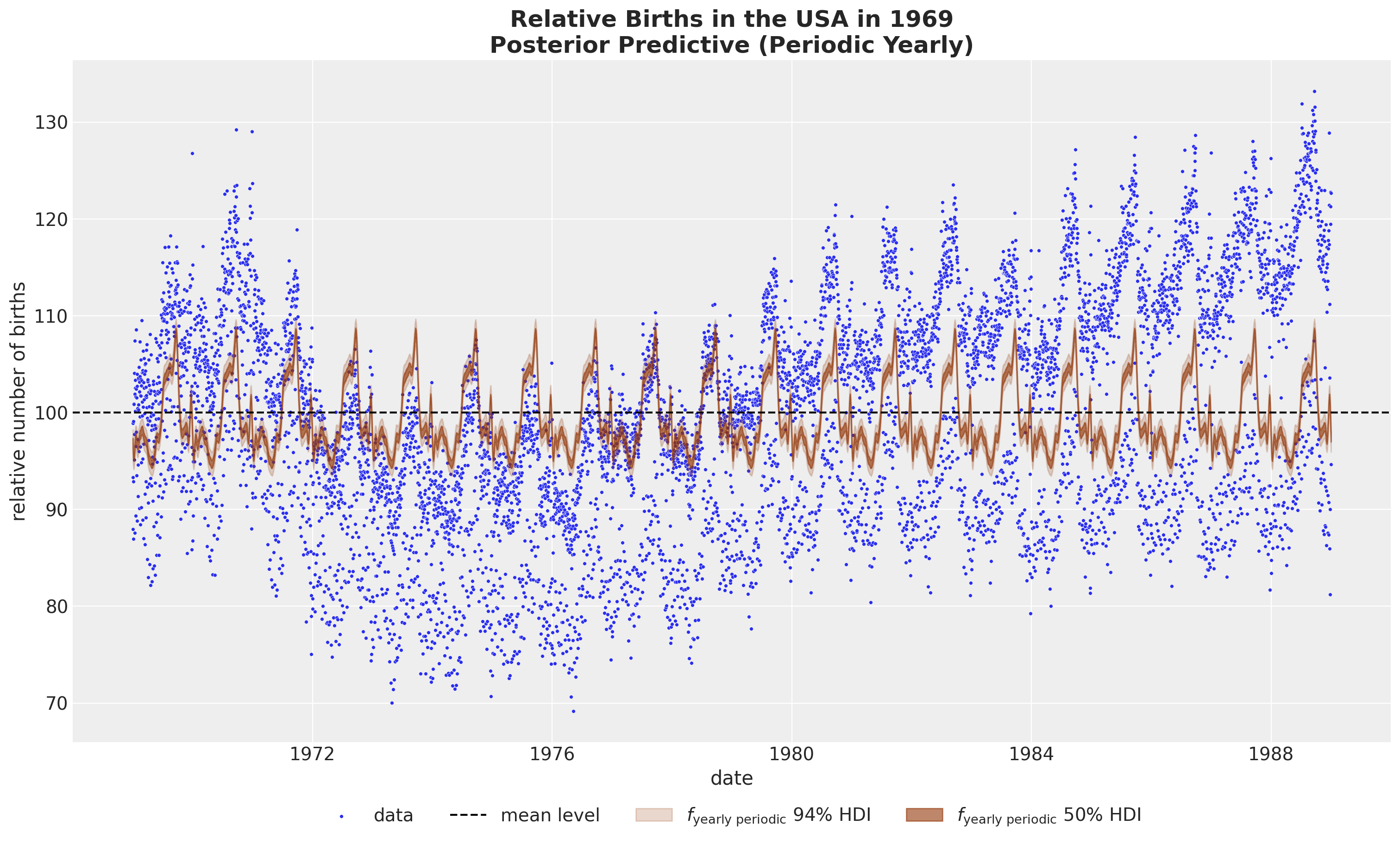
We use a Gaussian process with a periodic kernel*.

HSGP Model - Weekly Seasonality

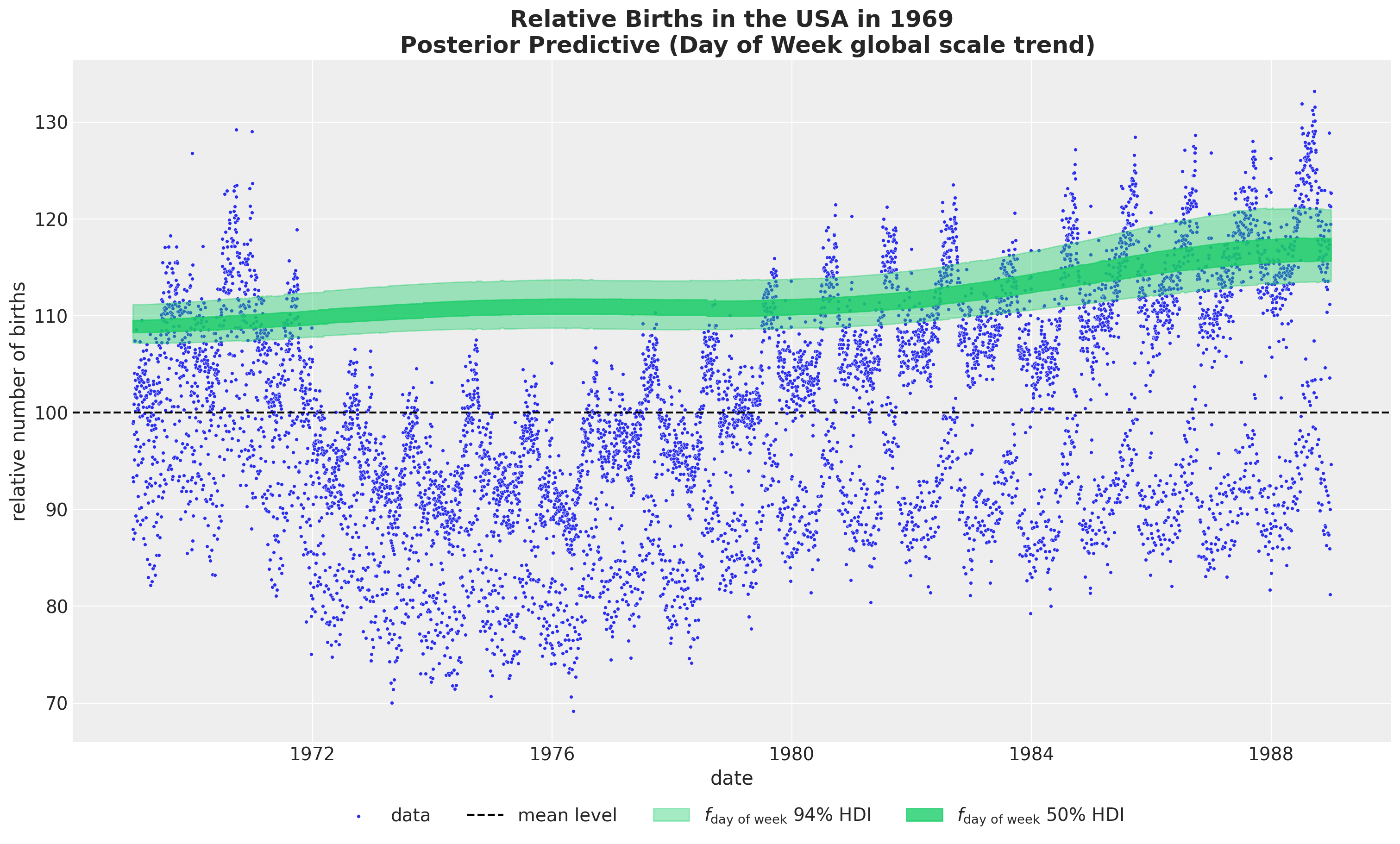
We use a ZeroSumNormal distribution to capture the relative difference across weekdays. We couple it with a multiplicative factor parametrized by a Gaussian process.

HSGP Model - Special Days

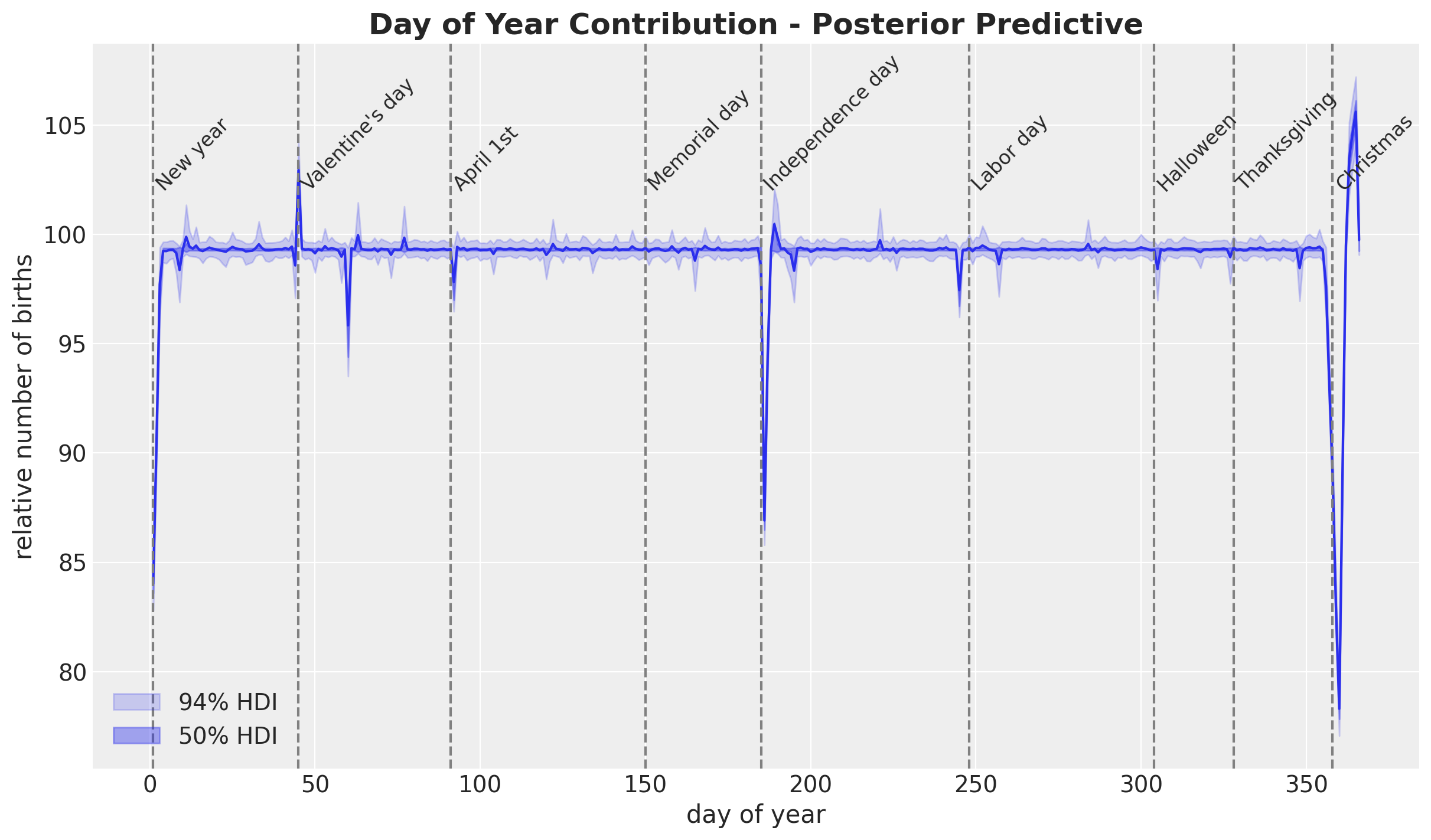
We use a StudentT distribution over the day_of_year2.

References

Gaussian Processes

HSGP Approximation

References

Birthdays Dataset

Spectral Theory

Thank you!

juanitorduz.github.io